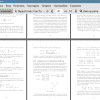
Тема: Динамические сетевые игры с попарным взаимодействием
Закажите новую по вашим требованиям
Представленный материал является образцом учебного исследования, примером структуры и содержания учебного исследования по заявленной теме. Размещён исключительно в информационных и ознакомительных целях.
Workspay.ru оказывает информационные услуги по сбору, обработке и структурированию материалов в соответствии с требованиями заказчика.
Размещение материала не означает публикацию произведения впервые и не предполагает передачу исключительных авторских прав третьим лицам.
Материал не предназначен для дословной сдачи в образовательные организации и требует самостоятельной переработки с соблюдением законодательства Российской Федерации об авторском праве и принципов академической добросовестности.
Авторские права на исходные материалы принадлежат их законным правообладателям. В случае возникновения вопросов, связанных с размещённым материалом, просим направить обращение через форму обратной связи.
📋 Содержание
Цели и задачи 8
Апробация работы 9
1 Динамические сетевые игры 11
1.1 Двухшаговые игры 11
1.1.1 Выбор управления 12
1.1.2 Кооперация в двухшаговых играх на втором шаге 14
1.1.3 Кооперация в двухшаговых играх на обоих шагах 16
1.1.4 Динамически устойчивые и сильно-динамически устойчивые решения 17
1.2 Динамические игры с шоком 19
1.3 Стратегическая поддержка кооперации 21
2 Описание сетевой игры с попарным взаимодействием 23
2.1 Общие сведения 23
2.2 Характеристическая функция 24
2.2.1 Пример построения характеристической функции 27
2.3 Другой способ построения характеристической функции 28
2.3.1 Пример построения харакетристической функции 30
2.4 Выпуклость игры 31
3 Решение сетевых игр с попарным взаимодействием: Вектор Шепли 34
3.1 Вектор Шепли для сети-звезда 34
3.2 Динамическая устойчивость вектора Шепли 37
3.2.1 Дилемма заключенного 39
3.2.2 Динамически неустойчивый вектор Шепли 41
4 Решение сетевых игр с попарным взаимодействием: C-ядро 44
4.1 Сильная динамическая устойчивость С-ядра 47
4.2 Пример сильной динамической устойчивости ядра 49
Заключение 52
Список литературы 54
📖 Введение
Согласно определению, приведенному Г. Оуэном, [5] теория игр — раздел прикладной математики, исследующий модели принятия решений в условиях несовпадения интересов сторон (которые называются игроками), когда каждая сторона стремится воздействовать на развитие ситуации в собственных интересах. Кооперативной называется игра, в которой группы игроков — коалиции — могут объединять свои усилия для достижения наилучшего результата.
Теория графов с точки зрения теоретической дисциплины может рассматриваться как одна из частей дискретной математики, исследующий свойства конечных множеств с заданными отношениями между элементами [3].
Теория графов с точки зрения прикладной дисциплины, позволяет описывать и исследовать многие технические, экономические, биологические и социальные системы. Подробно описаны методы дискретной математики, моделирующие процессы произвольной природы, в том числе используя графы, Ф.С. Робертсом в книге [14]. Начало этой науки — теории графов — было положено Эйлером, при решении известной многим задачи о кенигсбергских мостах (как пройти по всем семи мостам, не проходя ни по одному из них дважды). Позднее теория графов применялась Кирхгофом при исследовании им электрических сетей, Кели в органической химии, Гамильтоном для решения головоломок и многими другими математиками и специалистами, занимающимися картографией и раскраской карт. Решение Эйлера задачи о мостах совсем недавно было применено для оптимизации движения подметальных машин в больших городах, что дало большую экономию топлива, в следствии чего так же улучшились экологические показатели региона.
Между теорией игр и теорией графов существует тесная взаимосвязь. Инструменты и результаты теории графов широко используются в задачах по теории игр:
• древовидный граф задает структуру принятия решений в игре в развернутой форме [7],
• граф, где вершины — игроки, задает структуру всевозможных коалиций [4],
• граф отражает постоянные или временные связи между игроками,
• на графе в дискретном времени осуществляется "игра поиска" (вершины— позиции игроков, ребра — возможные пути переходов) [6].
Отдельно следует выделить теорию сетевых игр — относительно молодой (развивающийся с конца 70-х годов прошлого века) раздел теории игр, акцентирующий внимание как раз на формировании сетевых структур — устойчивых связей между игроками — в условиях несовпадения интересов. Точнее употреблять термин игра формирования сети, результатом которой является сеть, устанавливающая взаимосвязи между игроками. Далее рассматриваются так называемые "игры на сетях", где сеть уже является фиксированной, и не подлежит дальнейшим изменениям [24].
Основополагающим понятием любой игры является понятие выигрыша. В кооперативных играх важнейшей частью исследования является рассмотрение возможности создания коалиций и предложение по корректному распределению суммарного кооперативного выигрыша между игроками. Для этого наиболее удобен аппарат характеристических функций, показывающий возможности коалиции и являющийся основой для построения схем распределения суммарного выигрыша, приемлемых для игроков- участников. Достаточно полно по вопросам описания и решения кооперативные игры исследуются в книге С.Л.Печерского и Е.Б.Яновской [13]. В более поздних работах Печерского решается вопрос о применении пропорционального дележа для игры многих лиц и для игр с нетрансферабельной полезностью.
Несмотря на то, что теория кооперативных игр непрерывно развивается, вопрос о разделении выигрыша коалиций во многих постановках по- прежнему открыт. В реальной жизни люди постоянно сталкиваются с ситуациями, в которых они взаимодействуют с кем-либо через посредников. Иными словами, даже работая с крупными компаниями, взаимодействие сводится к решению вопросов один на один с посредником, представителем компании. Это один из многих примеров попарного взаимодействия между игроками. Впервые в теории игр попарное взаимодействие упоминается в работе [21]. В некооперативной игре с попарным взаимодействием исследуется существование равновесия по Нэшу, а так же время его нахождения. Попарное взаимодействие было так же рассмотрено на примере распространения информации и дезинформации в социальных сетях в работе [15]. Однако все эти работы относятся к некооперативным играм. Понимая актуальность данной темы, автором работы была выбрана для исследования структура сетевых игр с попарным взаимодействием игроков в применении к кооперативным многошаговым играм. После исследования кооперативного поведения, очень важно рассмотреть вопрос о том, следуют ли игроки принятым в начале игры кооперативным соглашениям на следующих шагах игры. Если найденное решение обладает свойством динамической (сильно-динамической) устойчивости, у игроков нет никаких причин отклоняться от принятых соглашений. Понятие сильной динамической устойчивости впервые было введено в [9]. Зачастую решения кооперативных игр не обладают этим свойством. Тогда возникает необходимость предупредить возможное отклонение игроков от кооперативного поведения. Процедура распределения дележа (ПРД) — это структура выплат, которая обеспечивает реализацию решения — была введена с целью предотвратить отклонения игроков в работе [11].
Работа имеет следующую структуру: в первой главе приводится краткий обзор истории исследования динамических сетевых игр — различные модели кооперации и поведения игроков.
Во второй главе приводится общее построение математической модели попарного взаимодействия игроков на сети на примере двухшаговой игры. Описывается процесс построения характеристической функции и исследуются ее свойства. Так же рассматривается еще один, альтернативный способ построения характеристической функции в данной задачи, который приводит к аналогичному результату. В последнем параграфе второй главы приводится доказательство выпуклости игры в форме характеристической функции как для двухшаговой игры, так и для одношаговой подыгры, начинающейся со второго шага.
Третья и четвертая главы посвящены решению кооперативных сетевых игры с попарным взаимодействием игроков. В третьей главе в качестве решения используется вектор Шепли. Для особого типа сетей (сеть-звезда) сделано преобразование формулы компонент вектора Шепли, которое существенно снижает вычислительную сложность данного процесса. А именно, упрощенная формула не требует вычисления значений харакетристической функции для каждой коалиции, а только лишь для коалиций не более чем из двух участников. Так же в третьей главе рассматривается вопрос о динамической устойчивости вектора Шепли. Этот вопрос исследован на двух примерах: повторяющейся игре "дилемма заключенного"и примере общего вида. В первом случае показывается динамическая устойчивость вектора Шепли, во втором — неустойчивость.
В четвертой главе в качестве решения взято С-ядро. В силу того, что характеристическая функция выпукла, сильно возрастает значимость этого принципа оптимальности для данного класса задач. С-ядро для сетевых игр с попарным взаимодействием исследуется на примере игры трех лиц. Построен общий вид ядра для двухшаговой игры и одношаговой подыгры, начинающейся со второго шага. Исследован вопрос о сильной динамической устойчивости С-ядра. Выведены условия, накладываемые на матрицы выигрышей, гарантирующие сильную динамическую устойчивость С-ядра в данной задаче.
✅ Заключение
В ходе работы были получены следующие результаты:
• Построена математическая модель сетевых игр с попарным взаимодействием.
• Приведены два способа построения характеристической функции, каждый из которых приводит к одинаковому результату. Оба способа проиллюстрированы численными примерами.
• Исследованы свойства характеристической функции в игре с попарным взаимодействием, в частности, доказана выпуклость игры в форме характеристической функции.
• Исследованы методы решения кооперативных сетевых игр с попарным взаимодействием.
• Для особого класса сетей (сеть-звезда) произведено преобразование формулы компонент вектора Шепли, существенно снижающее вычислительную сложность процесса поиска решения.
• Рассмотрен вопрос о динамической устойчивости вектора Шепли на примере повторяющейся игры «Дилемма заключенного» и примере общего вида. В первом случае показана динамическая устойчивость вектора Шепли, во втором — неустойчивость, и способы преодоления этой трудности.
• Так же в качестве решения рассмотрено С-ядро на примере игры трех лиц. Построен общий вид ядра, исследован вопрос о сильной динамической устойчивости решения, и найдены условия для этого. Полученный результат проиллюстрирован примером.
• Все полученные результаты прошли аппробацию на международных научных конференциях и семинарах.