Тема: Аномальные эффекты скоростной зависимости прочности при откольном разрушении
Закажите новую по вашим требованиям
Представленный материал является образцом учебного исследования, примером структуры и содержания учебного исследования по заявленной теме. Размещён исключительно в информационных и ознакомительных целях.
Workspay.ru оказывает информационные услуги по сбору, обработке и структурированию материалов в соответствии с требованиями заказчика.
Размещение материала не означает публикацию произведения впервые и не предполагает передачу исключительных авторских прав третьим лицам.
Материал не предназначен для дословной сдачи в образовательные организации и требует самостоятельной переработки с соблюдением законодательства Российской Федерации об авторском праве и принципов академической добросовестности.
Авторские права на исходные материалы принадлежат их законным правообладателям. В случае возникновения вопросов, связанных с размещённым материалом, просим направить обращение через форму обратной связи.
📋 Содержание
Предельная динамическая прочность 5
Цель и методы исследования 6
Научная новизна и практическая ценность 6
1 Структурно-временной критерий 8
1.1 Определение инкубационного времени 9
2 Анализ динамической прочности бетона 11
2.1 Характеристики нагружающих импульсов при разрушении бетона по схеме Гопкинсона - Кольского 11
2.2 Скоростная зависимость прочности 13
2.3 Откольное разрушение 15
2.4 Эксперименты по отколу в бетоне 17
3 Механизм возникновения эффекта стабилизации скоростной зависимости прочности 20
3.1 Откольное разрушение при фиксированной амплитуде импульса напряжений 20
4 Заключение 22
Список литературы 23
📖 Введение
Первые исследования на эту тему продемонстрировали, что прочность материала не является постоянной величиной и растёт при увеличении скорости деформации. Необходимо уметь давать качественный прогноз для таких явлений. Так, например, знание о поведении механических конструкций в условиях ударно-волнового нагружения, позволит избежать их внезапного обрушения. С другой стороны, высокоскоростное нагружение может способствовать развитию более эффективных методов добычи полезных ископаемых.
Всё это говорит о том, что важно уметь предсказывать поведение материалов в широком диапазоне скоростей деформаций, поэтому существуют различные подходы для осуществления таких исследований. Изучение процесса разрушения на низких скоростях деформаций, порядка 10-6 —100 c-1 осуществляют с помощью гидравлических машин. Затем проводят эксперименты по схеме Гопкинсона-Кольского в диапазоне скоростей от 101 до 104 c-1. Достижение скоростей деформаций в интервале от 104 до 106 c-1 можно осуществить при проведении экспериментов на откол. Этот подход базируется на рассмотрении волновых процессов, протекающих в исследуемом материале. Сначала в образце возбуждают волну сжатия, которая, отражаясь от свободной поверхности, сменяет знак и преобразуется в волну растяжения. Комбинация волн, достигнув критического растягивающего значения, способна вызвать откол части образца вблизи свободной поверхности.
Для анализа процесса разрушения необходимо иметь критерии, которые достаточно полно описывают явления, наблюдаемые в экспериментах. На данный момент существуют множество различных динамических критериев разрушения [1]. Анализ откольного разрушения в работе проводится с помощью структурно-временного критерия [2,3]. Преимуществами данного подхода является относительная простота, в совокупности с возможностью прогнозирования множества эффектов, характерных для конкретного вида динамического воздействия.
В ряде работ [4], по анализу зависимости прочности от скорости деформаций, наблюдается эффект стабилизации прочности. Выражается это в том, что при превышении некоторого значения скорости деформации динамическая прочность перестаёт изменяться. Некоторыми исследователями данный эффект трактуется, как достижение “предельной динамической” прочности материала. Такой подход неверен вследствие сильной неравно- весности динамического процесса. Использование структурно-временного подхода позволяет рассчитывать скоростную зависимость прочности и объяснять её стабилизацию. Этот подход был успешно применен для объяснения наличия стабилизации прочности у алюминия, в случае откольного разрушения при воздействии лазерным излучением на образец [5].
Скоростная зависимость динамической прочности
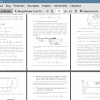
В работе [4] приведены материалы для которых при превышении некоторой скорости деформации, критическое значение напряжений перестаёт существенно изменяться. Авторы работы предлагают рассматривать три области для скорости деформирования (см. рис. 1).
Рис. 1: Зависимость динамической прочности от скорости деформации.
Области Qi и Q3 характеризуются слабой зависимостью от скорости деформации, а Q2 соответствует участку с высокой чувствительностью к скорости деформирования.
Данный эффект наблюдается для различных материалов. К ним относятся металлы [6-9], полимеры [10,11], хрупкие материалы [12] и т.д. На рисунке 2 приведены примеры для стали [6] и карбида кремния [12]. Наблюдение стабилизации прочности в большинстве случаев происходит при проведении экспериментов на откол.
Рис. 2: Зависимость динамической прочности от скорости деформации для некоторых материалов.
Цель и методы исследования
Целью настоящей работы является исследование зависимости предельных напряжений от скорости деформирования, а также объяснение явления стабилизации динамической прочности. Для построения модели, позволяющей описывать разрушение материалов в широком диапазоне скоростей деформации, применяется структурно-временной критерий. Данный критерий зарекомендовал себя в качестве удобного и практичного средства для описания квазистатического процесса разрушения, а также сверхбыстрого динамического [13-15]. При проведении расчетов использовались специально разработанные программы на языке Python.
Научная новизна и практическая ценность
Структурно-временной подход позволяет рассчитывать прочностные характеристики исследуемых материалов при квазистатическом и ударно-волновом видах нагружения. Применение структурно-временного критерия не требует задействования огромных вычислительных средств, следовательно может быть использовано повсеместно для расчета прочностных характеристик материалов.
В работе приведены схемы, позволяющие определять критические напряжения в широком диапазоне скоростей деформаций. Проведен анализ динамической прочности бетона. Исследованы характерные особенности разрушения для нагружающих импульсов, которые могут быть аппроксимированы кусочно-линейной функцией в виде треугольника.
Полученные результаты, могут быть полезны при решении таких инженерных задач, как расчет конструкций в условиях ударно-волнового воздействия на них, а также проектирование сооружений в областях, подверженных частым сейсмическим активностям.
✅ Заключение
Явление стабилизации скоростной зависимости прочности было исследовано на примере бетона. В результате была вычислена скоростная зависимость прочности в широком диапазоне скоростей деформации. Полученные результаты находятся в хорошем соответствии с данными из экспериментов.
Приведен пример откольного разрушения при фиксированной амплитуде, для которого при уменьшении продолжительности участка роста напряжений наблюдается, что критическое напряжение, вызывающее разрушение, практически перестаёт изменяться.
Для проведения расчетов были написаны программы на языке программирования Python. В их основу был положен критерий инкубационного времени. В случае откольного разрушения это позволяет определять критическое напряжение, время разрушения и соответствующее сечение образца.
Работа позволяет сделать вывод о том, что в случае высокоскоростных экспериментов основными параметрами характеризующими процесс разрушения являются амплитуда приложенного импульса, а также продолжительности участков роста и спада напряжений.
Практическая значимость исследования заключается в возможности прогнозирования поведения материалов в широком диапазоне скорости деформирования без задействования сверхмощных вычислительных средств. Рассмотрение проблемы разрушения с помощью структурно-временного подхода позволяет определить прочность материала для множества различных видов нагружения.