Тема: Исследование явных методов Рунге-Кутты повышенного порядка точности

Задачей Коши для системы обыкновенных дифференциальных уравнений описываются разные процессы в науке и технике. Получить аналитическое решение такой задачи можно только в малом числе возможных случаев. В связи с этим задача разработки и исследования численных методов решения задачи Коши является одной из наиболее главных в вычислительной матема­тике.
Сложность получения аналитического решения возникает и при дискре­тизации уравнений в частных производных методом прямых. В этом случае особенно актуальной становится проблема устойчивости метода. Как правило, число неизвестных в таких системах совпадает с числом узлов сетки, так что они имеют большую размерность. В связи с этим, для подобных систем пред­почтительно использовать явные методы, более простые и менее затратные в реализации, но, как правило, условно устойчивые.
В Главе 1 рассматриваются некоторые численные методы решения задачи Коши, а именно: метод рядов Тейлора, явные методы Рунге-Кутты. Рас­сматриваются такие понятия, как порядок точности и число этапов метода и их зависимость от набора параметров метода. Рассмотрена процедура по­строения методов. Приводятся определение функции устойчивости и области устойчивости. Приводятся формулы для методов повышенного порядка точ­ности.
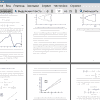
В Главе 2 рассматриваются явные методы Рунге-Кутты повышенного по­рядка точности. Выводятся системы условий порядка метода трех этапов для случаев неавтономного и автономного уравнений. Определяются вход­ные параметры. Производится наглядное сравнение функций устойчивости обычного метода и метода повышенного порядка точности. Предлагается осу­ществлять выбор входных параметров таким образом, чтобы площадь области устойчивости оказалась наибольшей.
В Главе 3 при решении тестовых задач показано, что предложенный под­ход к максимизации площади области устойчивости действительно позволяет улучшать практическую устойчивость методов.
Купить

Основные результаты проведенной работы:
1. Построены явные методы Рунге — Кутты повышенного порядка точности для случаев 2 и 3 этапов.
2. Определены оптимальные параметры трехэтапного метода для автономного и неавтономного уравнений.
3. При решении тестовых задач проведено сравнение методов повышенного порядка точности и обычных методов Рунге — Кутты.
По полученным результатам можно сделать следующие выводы:
1. При построении методов нет смысла рассматривать случай автономного уравнения.
2. При решении задач показано, что предложенный подход действительно позволяет улучшать устойчивость методов.
Купить