Введение 3
Постановка задачи 5
Обзор литературы 6
Глава 1. Исследование свойств траекторий удовлетворяющих принципу максимума 7
1.1. Свойства начального участка траекторий 7
1.2. Свойства траекторий содержащих участки совместного переключения управлений курсовым углом и скоростью 11
Выводы 15
Заключение 16
Список литературы 17
В современном мире люди каждый день управляют той или иной техникой или процессами. И так как прогресс не стоит на месте, то каждый день появляются новейшие объекты, которые требуют нахождения различных подходов к управлению ими. Поэтому вопрос управления сегодня весьма актуален. А так как люди не любят тратить свои усилия и ресурсы впустую, то они хотят управлять всем оптимально. Но эта проблема возникла уже очень давно и так как решение этой задачи далеко не всегда было тривиальным, то изобрели соответствующую математическую теорию, которая получила название «теория оптимальных процессов». Важнейшую роль в ней сыграл Л.С. Понтрягин, который сформулировал в 1958 году всем известный принцип максимума. Позднее принцип доказали Р.В.Гамкрелидзе и В.Г.Болтянский в частном и общем случаях соответственно.
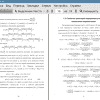
В жизни, мы стараемся закончить начатые дела, как можно раньше, поэтому на практике часто показателям качества решения является время, то есть мы хотим решить задачу быстродействия. Как известно, в случае линейных систем обыкновенных дифференциальных уравнений принцип максимума обеспечивает необходимые и достаточные условия для оптимальности решения. Однако же, когда возникает нелинейность, то мы прибегают к линеаризации, которая дает весьма хорошие результаты, но далеко не всегда. В таких случаях приходится прибегать к дополнительным исследованиям, опирающимся на вид и свойства конкретной нелинейной системы, благодаря которым иногда удается получить число точек переключения управления. В предлагаемой работе, приводится пример такого исследования. Нелинейная система обыкновенных дифференциальных уравнений описывает физическую задачу захода самолета при сильном боковом ветре на палубу авианесущего корабля или сближения двух самолетов для дозаправки, то есть задачу стыковки. В результате проведенного исследования были выявлены некоторые траектории движения данной системы, удовлетворяющие необходимому условию оптимальности.
Вопрос об оптимальности исследованных траекторий остается открытым. В дальнейших исследованиях нужно попробовать найти другие траектории и сравнить общее время движения. Также не получится аналитически определить точки переключения управлений, поэтому нужно воспользоваться для конкретной задачи численными методами, при этом следует заметить, что полученные свойства точек переключения управлений, существенно облегчают эту задачу.
