Методы анализа робастной устойчивости линейных систем с запаздыванием

Введение 3
1. Основные обозначения и определения 5
2. Математические модели эпидемии гриппа 7
2.1. Общие сведения о течении болезни 7
2.2. Статистические данные 7
2.3. Математическая модель эпидемии гриппа «Барояна-Рвачева» 8
2.4. Простейшая динамическая модель 9
3. Методы анализа робастной устойчивости линейных систем с
запаздыванием 11
3.1 Методы исследования 11
3.1.1 Метод функционалов Ляпунова-Красовского 11
3.1.2 Метод D-разбиений 16
3.2 Постановка задачи 18
3.3 Результаты 19
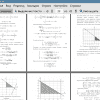
3.3.1 Скалярный случай 19
3.3.1 Матричный случай 26
Выводы 39
Список литературы 40
Приложение 41
Купить

Хотя отдельные уравнения с отклоняющимся аргументом появились в литературе во второй половине XVIII столетия, но систематическое изучение таких уравнений началось лишь с середины прошлого века [2], [5].
Частным случаем уравнений с отклоняющимся аргументом являются уравнения с запаздыванием [4]. Системы с запаздыванием находят много приложений в теории автоматического управления, в теории автоколебательных систем, при изучении проблем возникающих в биологии, химии, медицине, экономике и во многих других областях науки и техники.
Запаздыванием может быть время обработки информации или время химической реакции. В эпидемиологии, например, запаздыванием может оказаться инкубационный период заболевания или время, когда человек заразен. Так появляется задача анализа устойчивости системы с запаздыванием.
Методы прогнозирования инфекционной заболеваемости активно развиваются с начала XX века. Одна из работ на эту тематику была выполнена в 60-е годы в СССР акад. О. В. Барояном и проф. Л. А. Рвачевым. Ими была разработана новая методология математического моделирования эпидемий - эпиддинамика. Данная методология [2] основана на методе научной аналогии в отображении эпидемического процесса (процесс «переноса» возбудителя инфекции от больных к здоровым) с процессом «переноса» материи (энергии, импульса и др.) в уравнениях математической физики. В последние годы число работ на эту тему стремительно растет благодаря развертыванию информационных систем надзора и появлению больших объемов статистики [8], [9], доступной для анализа.
Таким образом, целью работы является изучение методов анализа оценки робастной устойчивости линейных систем с запаздыванием, рассмотрение примеров их применения, и нахождение допустимых областей изменения неопределенных параметров при анализе устойчивости линейных систем с запаздыванием. Кроме того, была построена математическая модель развития эпидемии гриппа в виде системы дифференциально-разностных уравнений запаздывающего типа.
Магистерская диссертация состоит из введения, трех глав, выводов, библиографического списка и приложения. Первая глава носит вспомогательный характер - в ней описаны основные обозначения и определения для дифференциальных систем с запаздыванием.
Вторая глава описывает математические модели эпидемии гриппа. В параграфе 2.1 описаны общие сведения о заболевании вирусом гриппа. Статистические данные, необходимые для исследования, приведены в параграфе 2.2. В параграфе 2.3 показана математическая модель эпидемии гриппа Барояна-Рвачева, а в параграфе 2.4 простейшая модель эпидемии гриппа.
В третьей главе проводится анализ областей устойчивости решений линейных систем с запаздыванием. В параграфе 3.1 описаны основные методы исследования: метод функционалов Ляпунова-Красовского (параграф 3.1.1), метод D-разбиения (параграф 3.1.2). В параграфе 3.2 идет постановка задачи, а в параграфе 3.3 её решение, разбитое на два случая: скалярный случай (параграф 3.3.1), матричный случай (параграф 3.3.2).
В приложении описана реализация в среде Matlab алгоритма нахождения допустимых областей устойчивости в пространстве неопределенных параметров.
Купить