Тема: Моделирование маршрутизации транспорта для решения задачи оптимизации работы логистической компании
Закажите новую по вашим требованиям
Представленный материал является образцом учебного исследования, примером структуры и содержания учебного исследования по заявленной теме. Размещён исключительно в информационных и ознакомительных целях.
Workspay.ru оказывает информационные услуги по сбору, обработке и структурированию материалов в соответствии с требованиями заказчика.
Размещение материала не означает публикацию произведения впервые и не предполагает передачу исключительных авторских прав третьим лицам.
Материал не предназначен для дословной сдачи в образовательные организации и требует самостоятельной переработки с соблюдением законодательства Российской Федерации об авторском праве и принципов академической добросовестности.
Авторские права на исходные материалы принадлежат их законным правообладателям. В случае возникновения вопросов, связанных с размещённым материалом, просим направить обращение через форму обратной связи.
📋 Содержание
Общая постановка задачи маршрутизации транспорта 6
Модификации и обобщения ЗМТ 7
Обзор типов ЗМТ 7
Неформальная постановка задачи 10
Формализованная постановка задачи 11
Алгоритмы решения ЗМТ 14
Точные комбинаторные методы 14
Методы локальной оптимизации 14
Конструктивные методы 15
Эвристические алгоритмы 15
Многофазные алгоритмы 16
Метаэвристические подходы 17
Описание программы 18
Общее описание 18
Получение данных 18
Преобразование и фильтрация данных 19
Кластеризация данных 19
Построение первичных опорных решений для каждого кластера 21
Улучшение первичных решений 27
Объединение кластеров в общее решение и его улучшение 31
Прочие алгоритмы, не использованные в построении решения 32
Возможные способы улучшения программы и алгоритмов 34
Результаты работы программы 38
Демонстрация вершин 38
Алгоритмы построения первичных опорных решений 40
Применение алгоритма Османа для первичных решений 45
Результат программы для различных первичных решений 49
Сравнение улучшения для различных первичных решений 53
Анализ результатов 54
Заключение 56
Список использованных источников 57
📖 Введение
Задача состоит не только в построение маршрутов, расписаний и графиков, но и в оптимизации затраченных на это ресурсов, построение наиболее выгодных маршрутов или иначе задача маршрутизация транспорта (Vehicle Routing Problem, ЗМТ).
ЗМТ - задача комбинаторной оптимизации, впервые была поставлена в 1959 году в работе [31]. Изначально задача была в определении маршрутов доставки некоего товара со склада множеству клиентов, и с тех пор было разработано множество подвидов и постановок, а также методов и алгоритмов ее решения. Задача определения оптимального расписания маршрутов относится к классу NP-трудных, поэтому большинство разрабатываемых алгоритмов ставят задачу поиска наилучшего суб-оптимального решения за наименьшее время.
Неформальная постановка задачи
Задача маршрутизации транспорта (ЗМТ) является обобщением задачи коммивояжера (ЗК). Отличие заключается в наличии нескольких коммивояжеров (называемых экипажами, транспортными средствами или ТС), пути которых пересекаются только в одной вершине - депо (остальные вершины называются клиентами). Именно она является вторым отличием от ЗК, фиксированная вершина графа, в которой начинается и заканчивается маршрут каждого ТС.
В качестве решения задачи необходимо составить несколько замкнутых путей, начинающихся в депо и покрывающих все вершины графа, чтобы значение интересующего нас функционала качества решения было как можно меньше. В роли функционала может выступать суммарная длина всех маршрутов, время движения по ним, предполагаемый объем затраченных денег, неустойка за опоздание доставки или сборки в вершине клиента.
Данная задача превосходит по сложности ЗК, а при наличии только одного экипажа является ею. Поэтому ЗМТ - NP-трудная задача.
Цель работы
Целью работы является решение задачи логистики для оптимизация вывоза твердых бытовых отходов (ТБО) на примере города Краснодар. В рамках чего исследуются различные постановки ЗМТ и алгоритмы их решения. А также объединение этих алгоритмов в ансамбль, налаживая взаимодействия алгоритмов. Тем самым получив гибкое настраиваемое программное средство, способную осуществлять построение расписания, не сильно отличающегося от оптимального, не только для конкретного взятого города, но и для большинство городов РФ и СНГ.
Методика исследования
В рамках решения задачи используются такие методы как, алгоритмы оптимизации путем локального, случайного и жадного поиска, математическое моделирование. А также используются различные программные средства для кодирования, получения, отображения и преобразования данных, в частности, Visual Studio, Anaconda3, Jupyter Notebook, OpenStreetMap с использованием языков программирования C++ и Python.
Практическая ценность
Данная работа предполагает создание удобного программного средства для решения задачи маршрутизации с различными требованиями и условиями. Полученное программное средство способно решать задачи логистики не только для вывоза твердых бытовых отходов, но и в целом составлять расписания доставки или сбора с оптимизацией длин полученных маршрутов (но не времени).
✅ Заключение
Основной подход к решению ЗМТ эвристические и метаэвристические алгоритмы. Для каждой конкретной формулировки ЗМТ подбираются определенные алгоритмы, которые не просто способны найти допустимое решение, но будут достаточно эффективны.
В процессе работы была сформулирована постановка задачи, отвечающая требованиям предметной области, а именно построение маршрутов для сбора и вывоза ТБО, а также разработана программа, реализующая и совмещающая известные алгоритмы. За счет общего интерфейса алгоритмов, данная программа достаточно гибко и легко поддается модификации: добавлению новых алгоритмов, изменению старых, а также внесению изменений в логику программы.
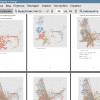
Результат работы был протестирован на данных о расположении площадок ТБО в городе Краснодар и проведен сравнительный анализ решений, построенных разными алгоритмами.