Введение 3
Постановка задачи 4
Обзор литературы 5
Глава 1. Математическая модель 7
1.1. Мгновенная выдачи товара 7
1.1.1 Вероятности состояний 7
1.1.2 Функция прибыли 9
1.2. Не мгновенная выдача товара 13
1.2.1 Вероятности состояний 13
1.2.2 Функция прибыли 15
Глава 2. Имитационное моделирование 16
Глава 3. Численные эксперименты 19
3.1. Мгновенная выдача товара 19
3.1.1 Интенсивности потоков товара и покупателей равны между собой 19
3.1.2 Интенсивности потоков товара и покупателей не равны между собой 20
3.1.3 Интенсивности потоков не известны 21
3.2. Случай не мгновенной выдачи товара 22
3.2.1 Оптимальный размер склада 22
3.2.2 Интенсивности потоков товара и покупателей не известны 23
Заключение 25
Список литературы 26
С ростом потребностей современного человека растет необходимость развития потребительской сферы. К потребительской сфере в данном случае относятся оптово розничные магазины, места общественного питания и т.д. А сложившееся в последние года эпидемиологическая ситуация дала толчок к развитию интернет-магазинов.
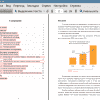
По оценке Data Insight в 2021 году доставлено 1570 млн отправлений, рост относительно 2020 года составил 78%
Рисунок.
Для интернет-магазинов, да и любого другого предприятия важную роль играет место хранение товаров, ресурсов. Склады представляют собой сложный элемент, отвечающий за снабжение и сбыт, и от них зависит качество и эффективность обеспечения потребителей необходимыми ресурсами. Актуальность выбранной темы заключается в том, что складская деятельность играет большую роль в успешном функционировании любого предприятия.
Каждая компания заинтересована в получении большей прибыли. Существует множество методов увеличить продажи или минимизировать издержки. Помимо этого можно анализировать логистику склада и улучшать его внутреннее устройство, а не внешние параметры.
В данном исследовании склад - это помещение для хранения, которое получает доход от продажи единицы товара. При этом имеются следующие затраты: на содержание помещения, на хранения единицы товара, на штрафы за переполнение.
Цель исследования заключается в том, чтобы вывести зависимость прибыли от объема склада, интенсивности потока товаров и покупателей. Найти оптимальные значения переменных, максимизирующих прибыль.
В работе рассматривалось два случая: обслуживание покупателей проходит мгновенно, на обслуживание требуется время. Для каждой задачи проводились следующие этапы:
1. Определить СМО, найти вероятность всех состояний системы.
2. Построить математическую модель - найти функцию прибыли.
3. Провести имитационное моделирование.
4. Провести численные эксперименты:
• Сравнение аналитического и имитационного решения.
• Поиск оптимальных значений для различных начальных данных.
Реализация численных экспериментов для тестовой задачи проводилась на Python. Ссылка на код программы: https://github.com/Fran-Tini/ Magistracy.git
Была рассмотрена задача нахождения прибыли склада в зависимости от объема склада, от интенсивности входящих потоков товаров и покупателей, от затрат на хранение товара и аренды склада, а также в зависимости от штрафов, накладывающихся за переполнение. Рассмотрено два случая:
1. Покупка товара происходит мгновенно. Люди могут выстраиваться в бесконечную очередь. Вероятность встать в очередь зависит от её длины (f (x) = 1/(x + 1)).
2. На обслуживание клиента требуется время. В этом случае очередь покупателей ограничена числом п.
Обе задачи решались на основе теории систем массового обслуживания. Для каждого случая построена математическая модель. С помощью имитационного моделирования показано, что математическая модель хорошо отражает реальное поведение системы.
Проведены численные эксперименты, в ходе которых проводился анализ функции прибыли для различных начальных данных. Найдены оптимальные значения объема склада и интенсивности потоков, которые дают наибольшую прибыль.
