1 Введение 2
2 Постановка задачи 4
2.1 Исследование сеточной сходимости 5
3 Математическая модель многокомпонентного реагирующего газа 6
3.1 Основные газодинамические уравнения 6
3.2 Осреднение по Фавру 9
3.3 Модель турбулентности Спаларта-Аллмареса 10
3.4 Уравнение диффузии 11
3.5 Двухтемпературная модель 14
3.6 5-ти компонентный реагирующий воздух 15
4 Численные методы 17
4.1 Метод конечных объемов 17
4.2 Охема на основе метода Годунова 17
4.3 Схема AUSM 18
5 Результаты численного моделирования 22
5.1 Поле распределения параметров при параметрах входного потока 22
5.2 Сравнение с экспериментальными данными и моделью совершенного газа 25
6 Заключение 27
Список литературы 30
Гиперзвуковое течение газа - сложное явление, сопровождающееся рядом особенностей, среди которых значительный рост температуры за фронтом головной ударной волны, сильное торможение потока внутри ударного слоя и аэродинамический нагрев поверхности. Такие процессы возникают в результате движения газа со скоростью, превышающей в пять раз скорость звука. Гиперзвуковые потоки газа могут быть созданы в различных условиях, например, при полете космических аппаратов в атмосфере Земли или при испытаниях гиперзвуковых летательных аппаратов.
Одной из особенностей гиперзвукового течения газа является возникновение ударной волны, которая формируется перед телом, движущимся с гиперзвуковой скоростью. При этом газ сжимается и нагревается до очень высоких температур.
Исследования гиперзвуковых течений газа является необходимыми для развития ракетостроения и аэродинамики. Гиперзвуковые двигатели и летательные аппараты позволяют достигать очень высоких скоростей, это особенно актуально для космических полетов и исследований других планет.
Таким образом, исследование данного явления необходимо для развития различных областей науки и техники. Его изучение и развитие технологий связанных с гиперзвуковыми потоками газа позволяют расширять границы нашего знания и открывать новые возможности для человечества.
Экспериментальное моделирование таких явлений является достаточно сложным и затратным с точки зрения ресурсов и времени процессом, а зачастую возможность полного моделирования условий натурного обтекания в ударных трубах и совсем исключается. С развитием электронно-вычислительной техники и в связи с перечисленными выше причинами методы численного моделирования приобретают важное значение. При этом стоит сказать, что сравнение с имеющимися результатами экспериментов, приобретает важное значение и является ключевым при оценке качества математической модели.
При исследовании гиперзвуковых потоков газов мы должны учитывать значительное влияние химических реакций, которые происходят в газе, что является отличием от сверхзвуковых потоков. Помимо этого, важным является учет внутренних степеней свободы молекул, так как они существенно влияют на характеристики потока.
Важную роль при моделировании гиперзвукового потока играет выбор газовой смеси. В данной работе использовалась 5-компонентная воздушная смесь. Численное моделирование гиперзвуковых течений связано с использованием сложной математической модели, включающей уравнения, описывающие пространственное течение вязкого сжимаемого газа, уравнения модели турбулентности, уравнения состояния, уравнения химической кинетики. Таким образом, по сравнению с моделью совершенного газа, неравновесные модели обсуждаемые в этой работе значительно сложнее, время на расчет до сопоставимой точности занимает в десятки больше времени, при этом приближение результатов к экспериментальным данным составляет порядка 10 %.
В данной работе обсуждается построение и реализация математической модели, предназначенной для численного моделирования гиперзвукового обтекания сферы с учетом неравновесных физико-химических процессов, протекающих в высокотемпературном воздухе. Численное моделирование осуществляется с использование программного комплекса Ansys Fluent.
Основной целью работы является исследование зависимости безразмерной толщины ударного слоя от скорости входного потока на основе данных, полученных в результате численных расчетов с использованием неравновесных моделей течения газа, и сравнение данного результата с экспериментальными данными и моделью совершенного газа.
Рассматриваются следующие модели:
1. Однотемпературная модель химической кинетики
2. Двухтемпературная модель химической кинетики
3. Модель совершенного газа
Результаты численного моделирования c применением данных моделей сравниваются с экспериментами [2], [3]. Работа выполнялась в рамках гранта Российского научного фонда, по результатам исследований были сделаны следующие публикации [14],[15].
Проведено моделирование задачи гиперзвукового обтекания сферы воздухом с использованием двухтемпературной модели неравновесной химической кинетики с 5-ти компонентным реагирующим воздухом. Были взяты начальные данные из работ [2],[3]. Модели с учетом физико-химических процессов, протекающих в газе, также сравнивались с моделью совершенного газа(без учета физико-химических процессов). Для решения данной задачи были построены 3 варианта вычислительной сетки и был сделан анализ сеточной сходимости, который показал, что оптимальное количество ячеек вычислительной сетки - 170000. Данная сетка использовалась в дальнейших расчетах. В качестве метода решения задачи о распаде произвольного разрыва в связи с рекомендациями, [9], был выбран метод AUSM, семейство данных методов является лучшим выбором при решении задач с сильными ударными волнами.
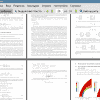
Исследована зависимость толщины ударного слоя от числа Маха на входной области. Произведено сравнение результатов расчета с использованием двухтемпературной и однотемпературной моделей с моделью совершенного газа и экспериментальными данными. Для двухтемпературной модели приведены поля распределения для газодинамических параметров в двух точках, было произведено сравнение полей распределения в зависимости от входных данных.
В целом, результаты, полученные с использованием модели совершенного газа без учета физико-химических процессов, показывают достаточно завышенные показатели толщины ударного слоя. Таким образом, в таких задачах, как, например, гиперзвуковое обтекание летательного аппарата при входе в атмосферу Земли необходимо применять более сложные модели, включающие в себя большее число уравнений. Хоть данный подход и является более затратным с вычислительной стороны, он дает значительно лучшее совпадение с экспериментальными данными.
Работа была проделана в рамках гранта, финансируемого Российским научными фондом. Большинство полученных результатов были опубликованы, [15], [14].
