1. Введение 3
2. Обзор литературы 4
3. Описание системы 5
4. Постановка задачи 10
5. Оценка допустимых возмущений 11
6. Примеры 19
6.1. Пример 1 19
6.2. Пример 2 21
7. Выводы 24
8. Заключение 25
Список литературы 26
Системы дифференциальных уравнений являются достаточно популярной темой для исследований. В ряде случаев даже незначительное изменение коэффициентов системы приводит к изменению каких-либо ключевых свойств системы. Таким образом, рассмотрение возмущенных систем становится актуальной проблемой.
Одним из основных методов в исследовании систем дифференциальных уравнений с запаздывающими аргументами является метод функционалов Ляпунова-Красовского. Целью данной работы является нахождение допустимых ограничений, при которых семейство возмущенных систем с запаздываниями удовлетворяет условию Ляпунова.
Основное содержание работы включает четыре раздела.
В разделе 3 содержится описание системы с запаздыванием и необходимые обозначения. В нем определяется понятие экспоненциальной устойчивости и рассматривается теорема Н. Н. Красовского, адаптированная для линейных систем. Она дает достаточные условия экспоненциальной устойчивости. В данном разделе вводится определение матрицы Ляпунова, приводится способ ее построения. Дается определение условия Ляпунова, а также теорема о необходимых и достаточных условиях его выполнения.
В 4 разделе приводится постановка задачи. Вводится семейство возмущенных систем с запаздывающими аргументами и матрицы, которые определяют возмущение системы.
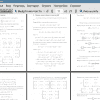
В разделе 5 приведена оценка допустимых возмущений. Введены вспомогательные леммы. Получена оценка разности матричных экспонент. Найдено неравенство, определяющее выполнение условия Ляпунова. Доказана теорема, дающая ограничения на допустимые возмущения системы.
В 6 разделе рассмотрены примеры. Для уравнения и системы с двумя запаздываниями найдены ограничения на допустимые возмущения.
Целью данной работы было получение условий, при которых возмущенная система удовлетворяет условию Ляпунова. В ходе исследования ограничения были получены. Также были рассмотрены примеры, для которых, используя полученные условия, были найдены допустимые значения изменения возмущений. Результаты данной работы были представлены на международной научной конференции аспирантов и студентов «Процессы управления и устойчивость»[9].
