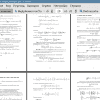
Тема: Категориальные методы анализа данных типа времени жизни
Закажите новую по вашим требованиям
Представленный материал является образцом учебного исследования, примером структуры и содержания учебного исследования по заявленной теме. Размещён исключительно в информационных и ознакомительных целях.
Workspay.ru оказывает информационные услуги по сбору, обработке и структурированию материалов в соответствии с требованиями заказчика.
Размещение материала не означает публикацию произведения впервые и не предполагает передачу исключительных авторских прав третьим лицам.
Материал не предназначен для дословной сдачи в образовательные организации и требует самостоятельной переработки с соблюдением законодательства Российской Федерации об авторском праве и принципов академической добросовестности.
Авторские права на исходные материалы принадлежат их законным правообладателям. В случае возникновения вопросов, связанных с размещённым материалом, просим направить обращение через форму обратной связи.
📋 Содержание
1. Основные понятия и определения 5
1.1 Введение в данные типа времени жизни 5
1.2 Точечные процессы 6
1.3. Представление данных с помощью точечных процессов 13
1.4 Описание цензурированных данных с помощью точечных процессов 15
2. Оценки Нельсона-Аалена и Каплана-Мейера, представление с помощью случайного процесса 16
2.1 Введение 16
2.2 Непараметрическое оценивание функции отказов 18
2.3 Оценка Каплана-Мейера 21
3. Состоятельность оценки Нельсона-Аалена и Каплана-Мейера 22
4. Мартингальная Центральная Предельная Теорема 28
5. Категориальный данные 31
5.1 Классические категориальные и из применение в анализе данных типа времени жизни 31
5.2 Категориальные тесты типа времени жизни 33
Список литературы 35
📖 Введение
В качестве основы для написания, были использованы следующие материалы:
1. Основные понятия и определения
Основан на материале: Fleming [1], Ширяев[2], Лебедев[3], Кокс,Оукс[5]
Даны вводные определения, необходимы для других разделов
2. Оценки Нельсона-Аалена и Каплана-Мейера, представление с помощью случайного процесса.
Основаной на материале: Fleming[1]
Даны базовые понятия оценок Нельсона-Аалена и Каплана-Мейера
3. Состоятельность оценки Нельсона-Аалена и Каплана-Мейера.
Основан на материале Fleming
Описаны состоятельность оценок Нельсона-Аалена и Каплана-Мейера
4. Мартингальная Центральная Предельная Теорема.
Основан на материале: Fleming[1]
5. Категориальный данные.
Основан на материале: Malov&O'Brien [4]
Описывается метод построения классических категориальных тестов и категориальных тестов типа времени жизни.