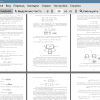
Тема: Задача управления движением двухкорпусного судна с малой площадью ватерлинии в условиях волнения
Закажите новую по вашим требованиям
Представленный материал является образцом учебного исследования, примером структуры и содержания учебного исследования по заявленной теме. Размещён исключительно в информационных и ознакомительных целях.
Workspay.ru оказывает информационные услуги по сбору, обработке и структурированию материалов в соответствии с требованиями заказчика.
Размещение материала не означает публикацию произведения впервые и не предполагает передачу исключительных авторских прав третьим лицам.
Материал не предназначен для дословной сдачи в образовательные организации и требует самостоятельной переработки с соблюдением законодательства Российской Федерации об авторском праве и принципов академической добросовестности.
Авторские права на исходные материалы принадлежат их законным правообладателям. В случае возникновения вопросов, связанных с размещённым материалом, просим направить обращение через форму обратной связи.
📋 Содержание
Постановка задачи 4
Обзор литературы 6
Глава 1. Математическая модель 7
1.1. Общие положения 7
1.2 Линейные уравнения движения 7
1.3 Применение теории потенциалов 8
1.4 Моделирование неопределенностей в коэффициентах 10
1.5 Моделирование волнения 13
Глава 2. Построение регулятора 16
2.1 Анализ устойчивости 16
2.2 H1 синтез 19
2.3 ц - синтез 23
2.4 Понижение порядка системы 24
2.5 Алгоритм решения задачи 27
Глава 3. Эксперимент и результаты 28
Выводы 32
Заключение 33
Список литературы 34
Приложение 36
📖 Введение
Однако, при определенных внешних возмущениях, СМПВ может терять устойчивость в вертикальной плоскости. В частности, при курсировании по морю при определенной скорости асимметричное распределение давления на погруженные корпуса вызывает дестабилизирующий момент, который может привести к тому, что судно может сильно сместиться по дифференту. Этот момент имеет название «момент Мунка» и его величина пропорциональна квадрату скорости судна.
В связи с этим было проведено исследование и доказано, что для СМПВ момент Мунка может быть компенсирован с помощью горизонтальных рулей и была сформулирована задача построения стабилизирующего регулятора для СМПВ. Однако, из-за высокой сложности построения математической модели и вычисления необходимых гидродинамических коэффициентов, оптимальное решение данной задачи до сих пор не было найдено. Кроме того, позднее было показано, что модель вертикального движения обладает высокой степенью неопределенности, сильно зависящей от скорости судна и характеристик моря.
Поэтому задача стабилизации СМПВ в условиях волнения не теряет актуальности и по сей день, кроме того, она влечет за собой дальнейшие работы по разработке управления для данного типа судов с использованием более сложных моделей.
✅ Заключение
Для построения регулятора, решающего поставленную задачу, использовались метод H1 синтеза, с помощью которого обеспечивались требования к качеству переходного процесса и ограничениям на управляющие элементы, а затем метод // - синтеза, с помощью которого обеспечивались робастные свойства замкнутой системы. В результате поставленная задача была решена - был получен регулятор, обеспечивающий робастную устойчивость и приемлемое качество переходного процесса в режиме волнения.
В дальнейшем приведенный алгоритм решения задачи и непосредственно регулятор, построенный для модели судна «DQ0 SWATH», могут быть применены при работе с более сложными математическими моделями, задающими движение других СМПВ в 6 степенях свободы. Также регулятор может быть использован как часть стабилизирующего регулятора при построении автопилота и системы управления курсом. В целом, данная работа представляет собой первый шаг в разработке полноценной системы управления СМПВ, решающей различные задачи мореходства судов данного типа.