Тема: ПРИМЕНЕНИЕ НЕЙРОСЕТЕВЫХ МЕТОДОВ ДЛЯ ВЫЧИСЛЕНИЯ ЛЯПУНОВСКИХ ПОКАЗАТЕЛЕЙ ПО ВРЕМЕННЫМ РЯДАМ ЭЭГ ДЛЯ ДИФФЕРЕНЦИАЦИИ РАЗЛИЧНЫХ СОСТОЯНИЙ СОЗНАНИЯ

В данной работе объектом исследования являются реальные временные ряды, а именно, - записи электроэнцефалограммы (ЭЭГ) медитаторов, как опытных, так и не опытных. Как известно, временной ряд порождается некоторой динамической системой, о которой мы, как правило, не обладаем знаниями. Поэтому для анализа исследуемых временных рядов нам необходимо уметь восстанавливать такие динамические системы. Подобные ситуации характерны для временных рядов различной природы – физических, биологических, финансовых.
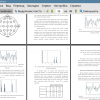
В настоящей работе используется метод классификации временных рядов и порождающих их динамических систем с точки зрения их нелинейно-динамических свойств. В качестве параметра для классификации в работе используются ляпуновские показатели [1,7], характеризующие динамические системы посредством описания разбегания близко расположенных друг к другу на аттракторе траекторий динамической системы. Наличие положительного показателя Ляпунова говорит о хаотичности исследуемой динамической системы [1,7].
Как было сказано выше, в данной работе исследуются временные ряды записей ЭЭГ медитаторов. В исследовании была использована база данных, предоставленная Научно-исследовательским центром «Экзиклуб». Она включает в себя записи из 19 каналов ЭЭГ для двух групп испытуемых (опытных и неопытных медитаторов) в состояниях фона с закрытыми глазами и медитации. Целью данной работы является нахождение количественного параметра для классификации медитаторов по временным рядам их записей ЭЭГ по группам – опытные и неопытные медитаторы. Таким предполагаемым параметром является показатель Ляпунова.
Вычислению ляпуновских показателей посвящено большое количество работ. В работе [1] авторы выделили два эффективных метода для оценки ляпуновских показателей: метод аналога и матричный метод. Первый метод основывается на измерении скорости разбегания близкий траекторий. При использовании матричных методов производится восстановление уравнений, задающих динамическую систему, и соответствующую им матрицу Якоби. Далее для определения ляпуновских показателей можно воспользоваться методом Беннетина, который описан в работе [2].
В настоящей работе использовался метод, разработанный в работе [3]. Данный метод заключается в вычислении спектра показателей Ляпунова с помощью комитета нейронных сетей и относится к матричным методам. Представленный алгоритм был протестирован на искусственных и реальных временных рядах [3].
Работа разбита на две главы. В главе 1 изложены необходимые для реализации исследования теоретические сведения. Даётся определение понятия динамической системы, локальных показателей Ляпунова (ЛПЛ) и глобальных показателей Ляпунова (ГПЛ). Также в главе 1 рассматривается используемый в работе метод определения ЛПЛ и ГПЛ при наличии знаний об отображении, задающем динамическую систему. В конце главы рассматривается метод определения ЛПЛ по временному ряду с использованием комитета нейронных сетей.
Глава 2 состоит из подробного описания проведенных в настоящей работе численных экспериментов. Сначала используемый метод тестируется на искусственных временных рядах, то есть временных рядах, порожденных известными динамическими системами, после чего метод применялся для анализа временных рядов записей ЭЭГ. Далее был рассмотрен вопрос о выделении ложных показателей Ляпунова (ЛПЛ) и их удалении. В конце главы представлены результаты исследования и их интерпретация.
Купить

Используемый в исследовании метод [3] определения ляпуновских показателей по временным рядам записей ЭЭГ оказался работоспособным. Сформулированная гипотеза исследования была подтверждена. Опытные медитаторы, имеющие стабильную динамику временных рядов записей ЭЭГ в состоянии фона с закрытыми глазами и состоянии медитации, при построении спектров ЛПЛ имели положительные значения ГПЛ. В случае испытуемых из группы неопытных медитаторов мы получили противоположные результаты – у них наблюдались отрицательные или близкие к нулю значения ГПЛ.
Таким образом, в результате исследования был выявлен количественный параметр (а именно, значение ГПЛ), который можно использовать при классификации медитаторов по группам опытных и неопытных. Более того, данный метод можно эффективно применять при исследовании реальных временных рядов другой природы – например, финансовых рядов.
Купить