Тема: АЛГОРИТМ МОНТЕ-КАРЛО ДЛЯ РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ МЕТОДОМ ЗЕЙДЕЛЯ

Метод Монте-Карло для решения системы линейных алгебраиче­ских уравнений рекомендуется использовать в том случае, если ее порядок достаточно велик [1]. В монографиях [1, 2] с помощью метода Монте-Карло вычисляется одна компонента вектора решения или скалярное произведение вектора решения и произ­вольного вектора. В работах [3-5] оценивается сразу весь вектор решений. В работе [3] используется стохастический метод итераций, причем математическое ожидание слу­чайного вектора очередной итерации совпадает с суммой соответствующего отрезка ряда Неймана. В статьях [4, 5] представлены алгоритмы Монте-Карло, позволяющие получать итерационное решение системы линейных уравнений при условиях более слабых, чем условия обычного метода Монте-Карло. В данной работе, в отличие от алгоритма в [3], особенность построения случайного вектора заключается в том, что математическое ожидание очередной итерации совпадает с итерацией Зейделя [6]. В дополнение к работе [7] доказывается существование и конечность предельных дис­персий случайного вектора решений системы.
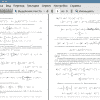
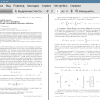
Пусть задана система линейных алгебраических уравнений вида
X = A ■ X + f, (1)
где A = [Aij ]лп — квадратная матрица, а X = (Xi,.. ,,Xn)T и f = (fi,..., fn)T — векторы.
В работе рассматривается алгоритм Монте-Карло, в основе которого лежит ме­тод Зейделя. Будем предполагать, что для нормы матрицы A выполняется условие
n
iiaii =maxI2A I <1 (2)
1 k=1
которое, в частности, обеспечивает сходимость метода Зейделя к единственному ре­шению системы (1) при любом выборе начального вектора [6].
Пусть задан начальный вектор X(0) = f, тогда на m-й итерации по методу Зей- деля [6] компоненты вектора X(m) вычисляются по формулам
X' = £AjX3(m) + ]^А^УХ(т-1) + fi, г = 1,...,n, m > I- (3)
j=1 j=i
Купить

Рассмотренный в работе метод Монте-Карло решения системы линейных алгебраических уравнений, основанный на итерационном процессе Зейделя, позволяет оценивать количество итераций, обеспечивающих нужную точность, и находить уравнения для ковариаций предельного по итерациям стохастического вектора. Ограниченность дисперсий компонент предельного вектора свидетельствует о стохастической устойчивости алгоритма. Найденные ковариации могут быть использованы для вычисления, например, дисперсии линейной комбинации решения.
Купить