1 Введение 2
1.1 Метод общей центральной точки 2
1.2 Формулы для годографов в случае симметричных отражений 4
1.3 Влияние анизотропии 6
1.4 Годограф ОПВ однократно отраженных волн 7
1.5 Годограф ОЦТ однократно отраженных воли 9
2 NIP теорема 12
2.1 Введение 12
2.2 Вывод уравнений XIP теоремы 12
3 Аппроксимация годографа ОЦТ волной NIP в изотроп­ном случае 14
3.1 Вывод формул 14
3.2 Численное моделирование и выводы 17
4 Аппроксимация годографа ОЦТ волной NIP в анизотроп­ном случае 17
4.1 Определение координат точки основания центрального луча 20
4.2 Определение координат точки отражения 22
4.3 Численное моделирование и выводы 23
5 Отражение от окружности 24
5.1 Постановка задачи 24
5.2 Численное моделирование и выводы 28
6 Приложения 32
6.1 Понятие анизотропии 32
6.2 Уравнение Кристоффеля и свойства плоских волн 33
6.3 Групповая (лучевая) скорость 35
6.4 Анизотропные системы симметрии 36
6.5 Трансверсально-изотропная среда 36
6.6 Распространение воли в трансверсально-изотропной среде 37
7 Заключение 41
Список литературы 44
Купить

1.1 Метод общей центральной точки
Одним из главных достоинств метода общей центральной точки (ОЦТ), также известного как метод общей средней точки (ОСТ), по сравнению с традиционным методом однократного профилирования по методу от­раженных волн (МОВ) является то, что он позволяет решать задачи вы­деления однократно - отраженных волн на фоне различного рода помех (как регулярных, так и нерегулярных). Одной из самых серьезных про­блем современной сейсморазведки является присутствие в записи много­кратно - отраженных волн. Их влияние на сейсмическую запись растет с увеличением времени регистрации. Поскольку ставится 'задача как повы­шения глубинности исследований, так и повышения качества волновой картины, что связано с прослеживанием полезных однократно - отра­женных волн на больших временах (t > 3 — 4 c) и уменьшения кратных, использование метода ОЦТ в ряде случаев становится более предпочти­тельным.
Специфические особенности метода ОЦТ основываются на направ­ленности системы наблюдения и статистическим эффектом суммирова­ния трасс [1]. Суть метода заключается в том, что сейсмические коле­бания, возбужденные в n источниках, регистрируются в n приемниках, расположенных таким образом по отношению к источникам, чтобы при условии горизонтального залегания границ раздела выполнялась реги­страция отраженных волн от общей для каждой границы раздела точки, В процессе выполнения обработки, исправленная на величину статиче­ских и кинематических поправок, запись суммируется. Поскольку опре­деление кинематических поправок происходит на основании приращении времен годографов полезных волн (в силу так называемого сейсмиче­ского сноса), оси синфазности последних трансформируются в прямые линии to = const, что обеспечивает суммирование колебаний практиче­ски исключая фазовые сдвиги. Отличающиеся по кинематике регуляр­ные волны-помехи суммируются с фазовыми сдвигами и соответственно, ослабляются.
Вопросы, связанные с построением моделей, описывающих данные метода отраженных волн (МОВ) как базы для метода ОЦТ, занимают центральное место в сейсморазведке. Начиная с пионерских работ [2, 15] были разработаны различные аппроксимационные формулы, описываю­щие времена прихода отраженных волн, включающие в себя члены вто­рого и четвертого порядка разложения времени в ряд Тейлора (по па­раметру выноса наблюдений) в предположении геометрии наблюдения ОЦТ и монотипных волн. Существенным ограничением является то, что все эти формулы применимы только для небольших выносов. С тех пор, для тех же условий наблюдения с целью использования больших выносов и учета эффекта возможной анизотропии среды, был предложен целый ряд улучшенных формул (аппроксимаций), уже включающих в себя сле­дующие члены разложения в ряд Тейлора [4, 5, 6, 7, 8, 9, 10] Похожие формулы, только с другим подходом к интерпретации пстиперболичсских членов были предложены в работе [11] для анализа времен прихода отраженных волн в случае азимутально-анизотропных сред. Всеобъем­лющий анализ различных аппроксимационных формул может быть най­ден в монографии [12].
Общей чертой, присущей большинству аппроксимационных формул, является то, что они так или иначе выражены через параметры цен­трального луча (луч, выпущенный к границе из центральной точки). Эти параметры связаны со степенью отклонения (которая определяет соот­ветствующий порядок производных) времени хода волны по произволь­ной траектории по отношению к времени хода волны вдоль центрального луча. Выбор конкретных параметров и их количество зависит от условий задачи для которых строится аппроксимация (прямая задача, обратная задача, миграция и др.)
Модель в которой центральный луч совпадает с лучом пулевого вы­носа (zero-offset ray) играет фундаментальную роль в сейсморазведке. В этом случае центральный луч является нормальным лучом к отра­жающей границе (для изотропных сред), а лучи, находящиеся в непо­средственной близости центрального носят название параксиальных. Си­стема этих лучей образует так называемый "нормальный сейсмический снос "(normal moveout) и известна как параксиальное приближение.
Важно отметить следующее. Несмотря па то, что поверхностные дан­ные наблюдений (записи сейсмограмм) содержат наряду с временами прихода сигналов также информацию об их амплитудах и фазах, все дальнейшие выводы и предположения будут учитывать только време­на прихода, так как базируются па высокочастотном приближении [13]. В данном приближении по аналогии с геометрической оптикой, распро­странение сейсмической энергии описывается с помощью лучей и вол­новых фронтов, пренебрегая информацией о фазе и амплитуде сигнала. Поскольку луч можно рассматривать как интегральную характеристи­ку волнового процесса, содержащую всю информацию о сто прошлом, то сто очень удобно использовать именно для описания времен прихода различных типов волн.
1.2 Формулы для годографов в случае симметрич­ных отражений
Для заданного положения рефлектора элементарное симметричное от­ражение - это процесс распространения волны при котором ход луча от источника до рефлектора полностью совпадает с ходом луча от рефлек­тора до приемника в обратном порядке. Рассматривая время прихода волны как функцию от координаты центральной точки и выноса (поло­вины базы наблюдений равной расстоянию между источником и прием­ником), легко заметить, что па основании принципа взаимности данная функция обязательно должна быть четной. Как следствие, любое разло­жение данной функции в ряд (по отношению к выносу) будет содержать только четные степени. Очевидно, что это условие выполняется для пер­вично отраженных волн. При этом, в процессе распространения могут происходить многократные отражения и образовываться обменные вол­ны как показано па Рис. 1.
Рис. 1: Симметричные отражения с образованием обменных волн (чер­пая линия) и центральный луч, соответствующий пулевому выносу (се­рая траектория), приходящий в точку нормального падения (Normal Incidence Point - NIP). Из работы [14].
В случае монотипных, однократно отраженных P - волн и горизон­тальной отражающей границы наиболее простым и известным выра­жением, описывающим сейсмический снос в геометрии ОЦТ, являет­ся так называемое уравнение нормального сейсмического сноса (Normal moveout equation):
T (h)2 = T0 + Ch2, (1.1)
где T - время хода, соответствующее пути источник-рефлектор-приемник, T0
h
сти от выбора системы координат) равный половине расстояния между C
„4 , ,
C = ■ ■ (1-2)
Vnmo
где Vnmo - скоростной параметр. Уравнение (1.1) представляет собой раз- h
стью до члена второго порядка. В данном случае это уравнение является гиперболической аппроксимацией времени и есть точное выражение для годографа в случае плоской, горизонтальной границы и однородной, изо­тропной среды.
Для больших выносов (превышающих расстояние до рефлектора) и случаев, где поведение годографа отличается от гиперболического, необ­ходимо учитывать следующие члены разложения [15]:
T (h)2 = T0 + Ch2 + Dh4, (1.3)
где коэффициент D отвечает за отклонение зависимости от гиперболи­ческой. Подробный анализ влияния члена четвертого порядка в случае слоистой изотропной среды может быть найден в [16].
Дальнейшая модификация уравнения (1.3) была представлена в ра­боте [17] в виде следующего выражения:
Dh4
T (h)2 = T0 + Ch2 + —h-, (М
1 + Eh
где C, D известные ранее коэффициенты, a E - вновь введенный пара­метр. Цель введения дополнительных параметров - улучшить результа­ты суммирования трасс при условии больших выносов, а также учета влияния анизотропии.
Также следует упомянуть, что в последнее время достаточно много внимания уделяется вопросу аппроксимации поверхностных годографов отраженных волн не обязательно ограничиваясь геометрией ОЦТ (Хоп- СМР moveout). Это связано с тем, что данных подход позволяет исполь­зовать всю информацию, накопленную в процессе наблюдений, для целей суммирования и последующей обработки [18]. В данном случае форму­ла для годографа в предположении гиперболической аппроксимации и монотипных волн может быть представлена в виде:
T(m, h) = (To + Am)2 + Bm2 + Ch2, (1.5)
где m обозначает координату центральной точки. Уравнение (1.5) спра­ведливо для произвольного расположения источника и приемника. Лег­ко заметить, что оно преобразуется в уравнение (1.1) для конфигурации ОЦТ при m = 0.
1.3 Влияние анизотропии
Метод отраженных волн и сто модификация в виде метода ОЦТ позволя­ет получать наиболее падежные и достоверные сведения для построения скоростных моделей с использованием данных поверхностных наблюде­ний как в изотропном, так и в анизотропном случаях. Если среда являет­ся анизотропной, то попытка аппроксимации годографа с использовани­ем изотропных параметров может привести к ошибкам в суммировании трасс и искажению сейсмических изображений (данный вопрос подроб­но обсуждается в работе [12]). Как следствие, понимание того каким образом анизотропия влияет па кинематику отраженных волн играет существенную роль в анализе и обработке сейсмических данных.
По аналогии с предыдущим разделом общее представление для вре­мени прихода отраженной волны можно записать в виде ряда:
t2 = Ao + A2h2 + A4h4 + ..., (1.6)
где h - вынос, а соответствующие коэффициенты даются формулами:
Ao = to', A2 =d(t2) . _ 1 d г d(t2) -
d(h2) h=o' 4 =2 d(h2) Ld(h2)-, h=0
Как говорилось ранее, наиболее часто употребительным параметром, характеризующим величину сейсмического сноса, является Vnmo (normal - moveout velocity), который определяет гиперболическую форму годо­графа отраженной волны па небольших выносах (по превышающих глубину залегания рефлектора).
t bhyp= t2 + 0 + V2 nmo
d(h2)
d(t2) h=0
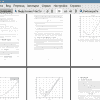
Если построить график времени прихода отраженной волны в коорди­натах t2 — h2, то коэффициент 1/V2mo будет определять начальный на­клон кривой. С увеличением выноса t2(h2) будет все более отличается от прямой линии в силу влияния следующих членов разложения - члена четвертой степени (A4h4) и следующих членов более высокого порядка.
Сейсмическая анизотропия вносит два главных вклада во временную картину отраженных волн. Первый - в отличие от изотропной среды Vnmo слоя) или от эффективной скорости Vrms для слоисто-однородной сре­ды. Это становится одной из основных причин получения искаженной информации при применении миграционных процедур по глубине и воз­никновения ошибок в определении глубин залегания сейсмических гра­ниц. Второй - анизотропия может существенно увеличить отклонения поверхностного годографа от гиперболической зависимости, поскольку даже в одном однородном, анизотропном слое годограф t(h) уже не опи­сывается гиперболической зависимостью [12].
1.4 Годограф ОПВ однократно отраженных волн
Так как, сейсмограммы, обрабатываемые по методу ОЦТ, представля­ют собой выборку каналов с сейсмограмм общего пункта возбуждения (ОПВ), полученных в процессе многократного профилирования МОВ, рассмотрим известное уравнение годографа однократно отраженной вол­ны для двухслойной модели среды с плоской отражающей границей. Ско­рость будем считать постоянной. Наблюдения проводятся в конфигура­ции ОПВ. В соответствии с [19] можно записать:
t(x) = — /x2 + 4dx sin ф + 4d2, (1.10)
где V1 - скорость, x - расстояние между источником и приемником, d - глубина залегания отражающей границы, определенная из центральной точки, ф - угол наклона границы. Данное уравнение есть уравнение годо­графа отраженной монотипной волны от плоской, наклонной границы, играющее важную роль в сейсморазведке. Его принято называть годо­графом общего пункта возбуждения (ОПВ). Оно представляет собой в координатах t — x уравнение гиперболы с осью симметрии в виде прямой линии: x = —2d sin ф. Уравнениями асимптот этой гиперболы будут две прямые линии:
x
t = ±V (1-11)
Для точек наблюдения, расположенных сравнительно близко к источни­ку (x < d) уравнение (1.10) может быть представлено в виде ряда по x
, . sin ф cos ф 2 sin 2ф cos 2ф 3 . .
t(x) =to + “Щ x + 2^ x2+ 4ЩЧ0 x + • • • (1'12)
Обычно бывает достаточным ограничиться первыми тремя членами ря­да, аппроксимируя гиперболический годограф квадратичной параболой.
Также при небольших углах падения отражающей границы (ф ^ 0) справедливо приближение:
t(x) = t0 + ^^ x + x2 + ... (1.13)
Vi 2 Vi t0
Точка минимума годографа, соответствующая минимальному време­ни пробста волны от границы и обратно, определяется координатами:
2d 2d cos ф
xmin : 7; tmin 77
sin ф V1
Важную роль в сейсморазведке МОВ играет время пробста волны от источника по нормали до границы и обратно, которое принято называть временем нормального отражения:
t(x)2d
= t0 =
Ж=0 V1
Важно отметить, что время нормального отражения будет минималь­ным временем годографа только для случая горизонтального залегания
(ф = 0)
С учетом введенного обозначения для плоской горизонтальной гра­ницы (ф = 0) уравнение годографа можно записать:
t(x) = г;;- Vx2 + 4d2 = 4 t0 + ^2
Vi Vi
В этом случае годограф отраженной волны имеет вид гиперболы, сим­метричной относительно начала координат.
Приведенное уравнение годографа общего пункта возбуждения со­вершенно аналогично по виду годографу общей точки приема в силу действия известного принципа взаимности, утверждающего, что замена источников и приемников не влияет на время распространения волны.
Годограф ОПВ приобретает более сложную форму, отличную от ги­перболы, когда отражающая граница имеет криволинейную форму [21]. Наименьшие искажения формы годографа отраженной волны наблюда­ются для выпуклых (в сторону поверхности наблюдений) сейсмических границ. Как правило, в этом случае нарушается гиперболическая форма годографа. Существенно большие искажения наблюдаются для случая вогнутых сейсмических границ. Степень этих искажений и их характер зависит от соотношения средней глубины залегания границы и радиуса ее кривизны. Когда радиус кривизны приближенно равен средней глу­бине залегания границы или меньше ее, то возникают сильные осложне­ния на годографе в виде появления на нем петель, скачков, разрывов и т.п. явлений.
1.5 Годограф ОЦТ однократно отраженных волн
Аналогично предыдущему разделу рассмотрим плоскую отражающую границу, залегающую под углом ф к горизонту. Покрывающая толща однородна и характеризуется постоянной скоростью V1.
В отличии от геометрии ОПВ начало координат поместим на поверх­ности наблюдений в точке O, которую будем называть общей средней точкой - ОСТ. Линию наблюдений на поверхности определяется осью Ox. Положительное направление оси Ox направим параллельно проек­ции линии падения отражающей границы на плоскость наблюдений. Глу­бина по нормали из центра системы координат до границы раздела равна d. В произвольной точке O на профиле наблюдений, имеющей координа­ту —1/2, поместим источник колебаний. В точке профиля с координатой 1/2 (расположенной симметрично относительно ОСТ) поместим прием­ник колебаний.
Уравнение годографа ОЦТ может быть получено из уравнения ОПВ путем сдвига системы координат. Временно совместим качало новой си­стемы координат с пунктом взрыва O1. Глубина по нормали в этой точке профиля будет равна:
d1 = d0 — 2 sin ф (1.16)
Как было показано в предыдущем разделе годографа уравнение ОПВ (1.10), определяющее время пробега волны по траектории O1DM в этой системе координат примет вид:
t(x) = —-^/x2 + 4d1x sin ф + 4d2
Подставим выражение для d1 из (1.16):
t(x) /x2 + 4x(d0 — X sin ф) + 4(d0 — X sin ф)2
v i у 2 2
— l4d2 + x2 cos2 ф (1.18) vi v
cos ф
С учетом следующих обозначений:
2d0 to = "VT
V = T_ cmp /
Выражение (1.18) преобразуется к виду:
t(x) = x2 cos2 ф
Vi2 x2
V2 cmp
(ПЭ)
Формула (1.19) представляет собой аналитическое выражение для годо­графа ОЦТ в случае плоской отражающей границы и однократно отра­женной, монотипной волны.
Анализ данного уравнения показывает, что годограф представляет собой гиперболу, симметричную относительно центральной точки. При фиксированном значении времени нормального отражения t0 форма (кру­тизна) годографа определяется единственным параметром Vcmp (cmp - common midpoint). On имеет размерность скорости, по существенно от­личается от истинной скорости: Vcmp - является фиктивным скоростным параметром, поскольку зависит от кажущегося угла падения границы вдоль линии наблюдения. Также следует заметить, что ввиду принципа взаимности форма годографа ОЦТ не зависит от знака угла.
При условии, что х2С°!2Ф < 1 выражение (1.19) может быть разложено
V1 С0
x
t(x)= to + 2 CV^x2 —1 Cost^x4 + ... (1.20)
При горизонтальном залегании отражающей границы отражение про­исходит от одной общей глубинной точки для каждой пар "источник - приемник". В то же время, при наклонном залегании границы для каж­дой пары "источник - приемник "положение точки отражения меняет­ся. Действительно, когда источник и приемник совпадают, то отраже­ние происходит от точки, определяемой основанием нормали к границе, проведенной из общей центральной точки. При ином расположении ис­точника и приемника точка отражения будет смещаться по отражающей границе в сторону ее восстания. Рис.2 иллюстрирует сказанное выше.
Рис. 2: Ход лучей при отражении от наклонной границы в геометрии ОЦТ. Отмечены различные точки отражения, соответствующие различ­ному расстоянию между источником и приемником.
Как показано в [19, 20] для оценки смещения точки отражения от основания центрального луча с использованием только геометрических соображений могут быть получены координаты фактической точки от­ражения для наклонной границы. Приведем здесь эти выражения:
X2 2 А
XD = — cos2 ф) sin ф
4d А)
zD = d cos ф — Х sin2 ф cos ф
4d
В тоже время величина смещения точки отражения относительно точки основания центрального луча согласно [21] пропорционально h2 и опре­деляется формулой:
. h2 sin2ф _
Р = 8d ,
где Др - смещение относительно точки нормального отражения, h - вы­нос, ф - угол наклона границы, d - глубина.
Купить