Введение 4
Искуственные нейронные сети 4
Задача распознавания образов 5
Искуственная нейронная сеть Хэмминга 5
Искуственная нейронная сеть адаптивной резонансной теории 7
Постановка задачи 8
Обзор литературы 8
1 Архитектура и алгоритм распознавания искусственной ней­ронной сети АРТ-1 10
1.1 Архитектура 10
1.2 Алгоритм распознавания 12
1.3 Возможные проблемы 15
2 Модификации для нейронной сети АРТ-1 17
2.1 Модификация, направленная на сокращение фазы поиска 17
2.2 Модификация, направленная на устранение фазы поиска 19
2.3 Сравнение 21
3 Программная реализация и тестирование 24
3.1 Особенности реализации 24
3.2 Перспективы 24
3.3 Изображения, используемые для тестирования 25
3.4 Критерии оценки качества нейронных сетей 26
3.5 Результаты тестирования 26
Выводы 26
Заключение 27
Литература 29
Купить

Искусственные нейронные сети
Широкий спектр современных задач, от идентификации частиц, воз­никающих в результате ядерных столкновений [1], до помощи в постанов­ке медицинских диагнозов [2], решается с использованием искусственных нейронных сетей. Также нейронные сети, из-за их биологического подобия, находят глубокий интерес среди исследователей из разных областей [3, 4].
Искусственная нейронная сеть — это множество взаимодействующих вычислительных элементов (нейронов). Каждый нейрон может выполнять лишь простейшие операции, однако, объединяя их в сети, можно проводить сложные распределенные вычисления. Наиболее интересной с точки зрения информатики является модель нейрона Маккалока-Питтса [5], согласно ко­торой, результатом работы нейрона является вещественная функция от ли­нейной комбинации сигналов других нейронов. Для решения конкретных задач коэффициенты линейной комбинации каждого нейрона подбираются в процессе специального алгоритма (обучения).
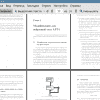
Распространен подход, в котором нейроны с одинаковой активацион­ной функцией и набором связанных нейронов объединяются в группы — слои. Хотя такой подход не соответствует реальным схемам взаимодействия нейронов в биологических нейронных сетях, он значительно упрощает про­ектирование и обучение искусственных. Следует отметить, что линейную комбинацию, вычисляемую в нейроне, легко представить в виде вектор­ного произведения. Тогда результатом работы нейронного слоя является вектор-функция от произведения матрицы коэффициентов (далее — мат­рица весов) на вектор сигналов от связанных нейронов (далее — входной вектор). Иллюстрация данного подхода приведена в формуле 1, здесь R — выход нейронного слоя, f (x) — активационная функция слоя, wi;j — коэф­фициент j-го нейрона для i-го входного сигнала, xi — i-й входной сигнал, M — количество нейронов в слое, N — количество входных сигналов.
f (!11x1 + • • • + !1N xN)
(1)
f (!M 1x1 + • • • + !MNxN) /
' Jvl X 1
К преимуществам нейронных сетей можно отнести единый подход к решению широкого спектра задач и возможность ускорения вычислений за счет массового параллелизма. Параллелизм обеспечивается независимо­стью работы каждого нейрона в слое.
Задача распознавания образов
Выбирая количество нейронных слоев, порядок их соединения и алго­ритмы обучения, нейронные сети можно настроить на решение различных задач: сжатие и архивация данных, прогнозирование (экстраполяция), ин­терполяция, аппроксимация, классификация и кластеризация. Особый ин­терес представляет задача распознавания образов [6] и, в частности, изоб­ражений. Перспективность данной задачи объясняется быстрым ростом количества производимой информации, в том числе графической. Эта ин­формация является отличным набором данных для обучения, тестирова­ния и применения нейронных сетей. В данной работе будет рассматривать­ся задача распознавания бинарных (черно-белых) изображений.
Искусственная нейронная сеть Хэмминга
Наиболее простой нейронной сетью для решения задачи распозна­вания бинарных изображений является сеть Хэмминга [5], основанная на одноименной метрике. Расстоянием Хэмминга между двумя элементами из пространства бинарных векторов фиксированной размерности называется количество различающихся компонент этих векторов.
Нейронная сеть Хэмминга состоит из двух слоев (сравнения, конку­ренции) и имеет следующий алгоритм функционирования:
1. Подготовка изображений. Входные изображения (матрица пикселей с высотой H и шириной W) раскладываются в вектор размерности N = HW. Один из цветов пикселей (например черный) представляется как 1, другой как —1.
2. Обучение. Множество из M эталонных изображений записывается в строки весовой матрицы слоя сравнения.
3. Сравнение. Описанная весовая матрица умножается на вектор, подле­жащий распознаванию, и получается вектор C = (Ci, ...,CM)Т, где Ci пропорциональна количеству совпавших пикселей в распознаваемом и i-м эталонном изображениях. Следует отметить, что величина Ci об­ратно пропорциональна расстоянию Хэмминга, и эталонный образ с максимальным Ci является наиболее близким ко входному в смысле меры Хэмминга.
4. Конкуренция. В слое конкуренции происходит поиск максимальной компоненты вектора C. Эталон, соответствующий данной компонен­те, является самым близким к входному образу в метрике Хэмминга. Это изображение и является результатом распознавания.
Преимущества
1. Использование простой метрики Хэмминга. Для сравнения, в нейрон­ной сети АРТ-1 используется мера сходства изображений, которая не является метрикой в математическом смысле.
2. Быстродействие. Наличие всего двух нейронных слоев обеспечивает малую вычислительную сложность по сравнению с некоторыми други­ми нейронными сетями.
Возможные проблемы
Отсутствие пластичности. В традиционной нейронной сети Хэм­минга не предусмотрена возможность обучения существующих эталонов и выделения новых категорий. В литературе такая проблема называется отсутствием пластичности. Причиной такого поведения является безуслов­ность определения победителя: во многих задачах требуется выделять но­вый эталон, если расстояние между распознаваемым и эталонным образом выше некоторого порога.
Искусственная нейронная сеть адаптивной резонансной теории
Адаптивная резонансная теория была разработана в 1987 году Сти­веном Гроссбергом и Гейл Карпентер. Существует несколько нейронных сетей, построенных в соответствии с этой теорией [7, 8] и одной из них яв­ляется АРТ-1 [9], предназначенная для распознавания бинарных изображе­ний и учитывающая недостатки сети Хэмминга. Архитектура и алгоритм АРТ-1 приведены в главе 1.
Преимущества
Существенным преимуществом данной сети является наличие пла­стичности. Также, в отличие от некоторых других нейронных сетей, на­пример персептрон [5], в АРТ-1 при обучении изменяется только эталон- победитель, не искажая все остальные. Данное преимущество называют свойством стабильности.
Возможные проблемы
1. Производительность. В силу особенностей алгоритма распознавания, вычислительная сложность АРТ-1 высока, по сравнению со многими другими нейронными сетями. Это может негативно сказаться, напри­мер, в задачах real-time распознавания [10].
2. Асимметрия нулей и единиц. В АРТ-1 при вычислении меры сходства используются только единичные элементы образов, и игнорируются нулевые. Это снижает качество распознавания в некоторых задачах.
3. Деградация запомненных образов. В силу необратимости алгоритма обучения запомненная информация может теряться.
4. Мера сходства изображений не является метрикой в математиче­ском смысле. Данный факт не является существенной проблемой, но использование простой меры Хэмминга облегчило бы тестирование и отладку нейронной сети.
Следует отметить, что приведены проблемы, выявленные при сравнении АРТ-1 с нейронной сетью Хэмминга. Также известны и другие проблемы, например отсутствие ассоциативной и распределенной памяти, но они не будут рассмотрены в рамках данной работы.
Купить