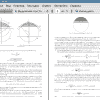
Тема: О ПРЕДСТАВЛЕНИИ ГРАВИТАЦИОННОГО ПОТЕНЦИАЛА НЕКОТОРЫХ МОДЕЛЬНЫХ ТЕЛ

Будем рассматривать гравитационный потенциал V компактного те­ла T во внешнем пространстве в сферических координатах г, 0, А. Для представления этого потенциала в [1-5] предлагается ряд Лапласа
VШ = M g (Ry+1 УДДХ).
R yr J
Здесь M — масса T, R — масштабный множитель, Yn —безразмерная сферическая функция; постоянная тяготения принята равной единице. В общем случае сфери­ческая функция зависит от 2п +1 параметров (коэффициентов Стокса). Разработа­ны и применяются на практике эффективные методы определения коэффициентов Стокса по спутниковым измерениям [6-8]. В случае осевой симметрии выполняется Yn(0, А) = Yn(d) = cnPn(cos д'), и остается лишь один параметр cn. Как обычно, Pn обозначает многочлен Лежандра со стандартной нормировкой Pn(1) = 1. Формула (1) принимает вид
VM) = M £ cddn+1 Pn(cos О). (2)
R у r J
n=0 ' '
Как принято в теоретических исследованиях, за R примем радиус объемлющей сфе­ры, содержащей Т внутри себя и имеющей с Т хотя бы одну общую точку.
Скорость сходимости ряда (1) существенно зависит от гладкости распределения масс в теле Т. Чем выше гладкость, тем быстрее сходится ряд, как это имеет место в теории приближения функций отрезками рядов [9-11]. Правда, в нашем случае поня­тие гладкости определяется довольно сложно [12]. Так, плотность может испытывать разрывы даже при пересечении поверхностей равной плотности, лишь бы сами они были достаточно гладкими. В то же время наличие ребер поверхности дТ даже одно­родного тела T катастрофически снижает гладкость распределения масс, поскольку теряет гладкость дТ, которую можно рассматривать как поверхность равной плот­ности.
Для приложений одним из наиболее интересных классов тел служит класс T компактных тел с ограниченной интегрируемой плотностью @(r, О, А), имеющей рав­номерно ограниченную вариацию вдоль любой окружности с центром в начале ко­ординат. Все реальные небесные тела принадлежат этому классу. Для тел Т -_ Т известна оценка [12]
C
Y < —2. (3)
Через C здесь и ниже обозначены различные постоянные, зависящие от свойств плот­ности q, (•) —чебышёвская норма (максимум модуля функции на сфере). Мы считаем п 1, так как Yo тождественно равно единице.
Заметим, что впервые подобная оценка (с делителем п2 вместо п5/2) получена М. С. Яров-Яровым [13].
В осесимметричном случае имеем
(Yn) = Щ (4)
Оценка (3) точна в следующем смысле. Существует тело Т -_ Т такое, что при некотором C справедливо неравенство (3), но при любом фиксированном а > 5/2 выполняется
sup па (Yn) = то. (5)
Несколько подтверждающих примеров приведено в [12]. В настоящей статье мы рас­ширим список примеров, по-прежнему ограничиваясь однородными телами враще­ния, для которых справедливо (4). В этих модельных примерах (для первых четырех коэффициенты Стокса cn взяты из [12]) тела слабо напоминают реальные планеты и спутники. Однако затем из них как из элементов мы строим более реалистичные фигуры.
Купить

Мы исследовали скорость сходимости ряда Лапласа нескольких модельных тел: полушар, шаровой сектор, цилиндр, конус, шаровой сегмент, сегмен­тированный шар. Во всех случаях (за одним исключением) скорость убывания {Yn} описывается неулучшаемой оценкой (3). Важную роль здесь играет фигура S — пе­ресечение границы дТ тела Т и объемлющей сферы S.
В примерах 1, 2, 5.1 фигура S состоит из части сферы S положительной пло­щади; граница S представляет собой ребро поверхности дТ. К этому же классу тел можно отнести и сегментированный шар, ребрами которого можно считать границы сегментов с разной плотностью.
В примерах 3, 4, 5.2 фигура S состоит из кривых, лежащих на сфере S и пред­ставляющих собой ребра поверхности дТ.
Исключением служит пример 5.3, в котором [Yn) убывают существенно быстрее согласно (9). В этом случае S — это одна точка, в которой дТ касается S, и в окрест­ности которой поверхность дТ аналитична. Интересно, что область сходимости ряда (1) — лежащая внутри S сфера S*, радиус которой равен расстоянию до ребра по­верхности дТ. Таким образом, и здесь сфера сходимости S* определяется ребром поверхности дТ, как и в предыдущих случаях.
Остался неисследованным случай, когда S состоит из конечного числа точек Ak, в окрестности которых дТ лежит внутри конуса с вершиной Ak с осью, проходящей через начало отсчета и углом полураствора, меньшим п/2.
Модельные тела — полушар, шаровой сектор, цилиндр, конус, шаровой сегмент — слабо напоминают реальные планеты и спутники. Сегментированный шар является более реалистичной фигурой для представления гравитационного потенциала небес­ных тел.
Купить