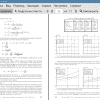
Тема: ВЛИЯНИЕ ПЕРЕМЕННОГО ДИАМЕТРА МОЛЕКУЛ НА КОЭФФИЦИЕНТ ВЯЗКОСТИ В ПОУРОВНЕВОМ ПРИБЛИЖЕНИИ
Закажите новую по вашим требованиям
Представленный материал является образцом учебного исследования, примером структуры и содержания учебного исследования по заявленной теме. Размещён исключительно в информационных и ознакомительных целях.
Workspay.ru оказывает информационные услуги по сбору, обработке и структурированию материалов в соответствии с требованиями заказчика.
Размещение материала не означает публикацию произведения впервые и не предполагает передачу исключительных авторских прав третьим лицам.
Материал не предназначен для дословной сдачи в образовательные организации и требует самостоятельной переработки с соблюдением законодательства Российской Федерации об авторском праве и принципов академической добросовестности.
Авторские права на исходные материалы принадлежат их законным правообладателям. В случае возникновения вопросов, связанных с размещённым материалом, просим направить обращение через форму обратной связи.
📋 Содержание
1. Введение 1
2. Модели потенциалов 2
2.1. Модель Тица—Хуа 2
2.2. Модель Морзе 3
2.3. Модель Канга—Кунца 3
2.4. Результаты сравнения потенциалов 3
3. Расчет коэффициента вязкости 5
4. Постановка задачи 5
5. Результаты 6
6. Заключение 9
Литература 9
ANNOTATION 10
References 10
📖 Введение
В работе [14] был предложен простой метод для получения приближенных оценок влияния молекулярного диаметра на коэффициент сдвиговой вязкости. Однако для расчета диаметра колебательно возбужденной молекулы использовалась модель [10], существенно переоценивающая размер молекул на верхних колебательных уровнях. В связи с этим расчеты приходилось обрывать при достаточно низких значениях колебательной энергии, что заметно ухудшает точность оценок. Целью настоящей работы является оценка вклада возбужденных состояний в коэффициент сдвиговой вязкости компонентов воздуха на основании более точных моделей потенциалов с учетом всех возможных колебательных состояний. Исследуется отношение коэффициента вязкости к соответствующему коэффициенту в основном колебательном состоянии для различных значений температуры, равновесных и неравновесных распределений.
✅ Заключение
Анализ результатов расчета отношения поуровневого коэффициента сдвиговой вязкости к коэффициенту вязкости для газа, состоящего из невозбужденных молекул, показал, что во всех рассмотренных случаях, включая сильнонеравновесные, эффект увеличения молекулы практически не влияет на вязкость, в среднем отклонение составляет лишь 1-2%. Некоторый эффект наблюдается только при очень высоких температурах для близких к равновесным колебательных распределений. Однако такие условия на практике реализовать достаточно сложно, поскольку в околорав- новесном высокотемпературном течении доля недиссоциирующих молекул пренебрежимо мала. Таким образом, нам удалось для широкого диапазона условий показать справедливость предположения о том, что при расчете поуровневых коэффициентов переноса зависимость сечения упругого столкновения от колебательного уровня можно не учитывать. Это позволяет обоснованно применять упрощенные алгоритмы расчета коэффициентов переноса.