АННОТАЦИЯ 1
1. ВВЕДЕНИЕ 1
2. КОЛЕБАНИЯ МЕМБРАНЫ С ЖИДКОСТЬЮ 2
3. КОЛЕБАНИЯ СТРУНЫ ПРИ НАЛИЧИИ СВЯЗИ 4
4. КОЛЕБАНИЯ СТРУНЫ ПРИ НАЛИЧИИ СВЯЗИ С УЧЕТОМ ПРИСОЕДИНЕННОЙ МАССЫ ЖИДКОСТИ 6
5. ПРЕОБРАЗОВАНИЕ СИСТЕМЫ (2.13) И ЧИСЛЕННЫЕ РЕЗУЛЬТАТЫ 7
ЛИТЕРАТУРА 9
ANNOTATION 10
REFERENCES 10
Введение. Рассматриваемая модельная задача относится к обширному классу задач динамической гидроупругости. К этим задачам приходим в судостроении, авиации, при транспортировке жидкостей, при описании природных явлений и во многих других случаях. Различные подходы к решению таких задач, а также обширную библиографию можно найти в монографиях [1—4]. В качестве первых исследований назовем работу Рэлея [5] о волнах в бесконечной пластине, контактирующей с жидкостью, и работу Лэмба [6] о колебаниях круглой пластины в воде. Колебания упругих тел в сжимаемой жидкости сопровождаются излучением звуковых волн [4], колебания пластин на поверхности жидкости порождают поверхностные волны [7]. Эти волны уносят энергию колебаний, что приводит к комплексному спектру. Спектр частот колебаний упругих контейнеров, содержащих идеальную несжимаемую жидкость, является вещественным и дискретным [1]. При этом, как правило, рассматриваются задачи, в которых жидкость имеет свободную поверхность [8, 9].
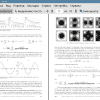
Ниже рассматривается контейнер в форме прямоугольного параллелепипеда, полностью заполненный несжимаемой жидкостью и закрытый упругой прямоугольной крышкой. Крышка моделируется упругой мембраной или пластиной с шарнирно опертыми сторонами. Изучается спектр частот свободных колебаний этой крышки (вместе с жидкостью) при условии, что при колебаниях объем жидкости под крышкой не меняется. Это условие порождает связь, которой должна удовлетворять форма прогиба крышки. При наличии аналогичной связи на форму прогиба также построен спектр частот колебаний струны и балки.
Близкая постановка задачи принята в [10]. В ней ограничение на форму прогиба крышки (пластины) не вводится, однако рассмотрение графиков собственных функций, приведенных в [10], говорит о том, что условие сохранения объема жидкости под крышкой выполнено. В рассматриваемых задачах предполагается, что характерный период свободных колебаний существенно больше времени пробега волны объемной деформации жидкости. Поэтому жидкость считается несжимаемой.
При выполнении работы рассматрен контейнер в форме параллелепипеда, заполненный идеальной несжимаемой жидкостью, закрытый упругой крышкой, которая моделируется мембраной или пластиной постоянной толщины. Также построен спектр частот малых свободных колебаний крышки с учётом присоединённой массы жидкости, движение которой предполагается потенциальным.
