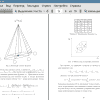
Тема: Распараллеливание метода декомпозиции области типа Дирихле-Дирихле

Для современных физических задач часто необходимо быстро ре­шать уравнения в частных производных. При этом физические задачи могут характеризоваться абсолютно разными уравнениями на разных областях. Хотелось бы иметь метод, позволяющий на параллельной ма­шине быстро решать подобные задачи, также учитывающий некоторые физические ее особенности, например, разнородность рассматриваемо­го материала.
В настоящее время наиболее популярными методами для численно­го решения уравнений в частных производных являются метод конеч­ных разностей или метод конечных элементов. Таким образом, решение уравнения в частных производных сводится к решению большой алгеб­раической системы уравнений. Размер системы зависит от плотности сетки. Столь плотные сетки (порядка миллиона узлов и больше) ока­зываются необходимы для получения достаточно точных физических параметров рассматриваемого объекта, например, напряжения. Эти си­стемы оказываются очень разреженными, и для их решения могут при­меняться различные методы, такие как метод LU-разложения, метод Якоби, метод Гаусса-Зейделя, варианты метода сопряженных гради­ентов. Также хочется иметь достаточно быстрый метод для решения больших СЛАУ, так как могут ставиться задачи мониторинга неко­торой физической системы в живом времени. Однако указанные вы­ше методы являются недостаточно хорошо гранулируемыми, поэтому отдельно хотелось бы выделить многосеточный метод, показывающий лучшую асимптотику на многопроцессорных системах.
Особенно хочется отметить метод декомпозиции области, исполь­зующийся для решения указанных систем линейных алгебраических уравнений и имеющий хорошие теоретические оценки времени испол­нения. Он может включать в качестве своей части различные методы, указанные выше. В данной работе исследуются его оптимальные пара­метры при различных входных данных.
Купить

В рамках данной работы был рассмотрен метод конечных элемен­тов. Для решения получившейся системы использовался метод деком­позиции области и многосеточный метод. Была реализована параллель­ная программа и запущена на вычислительном кластере.
Рассмотренный алгоритм позволяет быстро решать уравнение Пуас­сона. Также он показывает значительное ускорение при увеличении числа подобластей, что доказывает возможность его эффективной параллелизации и высокую гранулярность. Использование метода деком­позиции области может эффективно использоваться для быстрого чис­ленного решения эллиптических задач на параллельных компьютерах и кластерах.
Купить