Тема: Оптимальное планирование эксперимента для экспоненциальной регрессии
Закажите новую по вашим требованиям
Представленный материал является образцом учебного исследования, примером структуры и содержания учебного исследования по заявленной теме. Размещён исключительно в информационных и ознакомительных целях.
Workspay.ru оказывает информационные услуги по сбору, обработке и структурированию материалов в соответствии с требованиями заказчика.
Размещение материала не означает публикацию произведения впервые и не предполагает передачу исключительных авторских прав третьим лицам.
Материал не предназначен для дословной сдачи в образовательные организации и требует самостоятельной переработки с соблюдением законодательства Российской Федерации об авторском праве и принципов академической добросовестности.
Авторские права на исходные материалы принадлежат их законным правообладателям. В случае возникновения вопросов, связанных с размещённым материалом, просим направить обращение через форму обратной связи.
📋 Содержание
Постановка задачи ....................................................................................................................................................... 5
Глава I. Обзор литературы .......................................................................................................................................... 6
Глава II. Оптимальный план для регрессионного эксперимента .......................................................................... 10
2.1. Классическая схема регрессии ..................................................................................................................... 10
2.2. Нелинейная экспоненциальная регрессия .................................................................................................. 11
2.3. ЛокальноD -оптимальные планы для экспоненциальной регрессии ..................................................... 12
Глава III. Метод случайного поиска глобального экстремума на основе оценивания элементов матрицы
ковариаций ................................................................................................................................................................ 14
3.1. Простейший случайный поиск (слепой поиск) ............................................................................................ 14
3.2. Доказательство сходимости простейшего случайного поиска .................................................................. 15
3.3. Оценивание числа испытаний ...................................................................................................................... 16
3.4. Случайный поиск с “памятью” ...................................................................................................................... 16
3.5. Введение неравномерного распределения ................................................................................................ 17
3.6. Алгоритм метода случайного поиска с “памятью” ..................................................................................... 18
Глава IV. Метод Метрополиса для нахождения моды плотности распределения случайных величин ............ 25
4.1. Выборка с отклонением ................................................................................................................................ 25
4.2. Модифицированная выборка с отклонением ............................................................................................. 26
4.3. Метод Метрополиса ...................................................................................................................................... 27
4.4. Частный случай алгоритма Метрополиса .................................................................................................... 28
Глава V. Численные результаты ............................................................................................................................... 30
Выводы ....................................................................................................................................................................... 33
Заключение ................................................................................................................................................................ 34
Список литературы .................................................................................................................................................... 35
Приложения ............................................................................................................................................................... 39
Приложение 1. Моделирование равномерно распределенного вектора в заданной области .................... 39
Приложение 2. Метод Монте-Карло для оценки интегралов .......................................................................... 39
Приложение 3. Моделирование нормально распределенного случайного вектора [11] ............................. 41
1). Моделирование двумерного нормального распределения ..................................................................... 41
2). Моделирование многомерного нормального распределения ................................................................. 42
Приложение 4. Листинг программы. .................................................................................................................. 44
📖 Введение
витие математической теории оптимального эксперимента.
В условиях дороговизны экспериментов или при проведении экс-
периментов, которые невозможно воспроизвести повторно, требуется
предварительное планирование. Здесь важным для нас является поня-
тие имитационного эксперимента, направленного на изучение реально-
го процесса с последующим построением имитационной модели и по-
лучения реализаций некоторой случайной функции. Квалифицирован-
ное планирование приводит к сокращению времени, числа и стоимости
измерений, в повышении точности восстановления неизвестной зави-
симости, в возрастании достоверности полученных выводов.
Во многих областях науки, например, таких как ядерная физика,
спектроскопия, дистанционное зондирование атмосферы, регистрация
и анализ изображений, анализ состава веществ, оптические методы ин-
дикации неоднородностей и загрязнений среды, цветовые измерения и
т.д. возникают задачи восстановления распределений различной при-
роды и оценивания их параметров [17,24,26,28,38].
Когда создана математическая модель и выбран метод планиро-
вания можно приступать к имитированию эксперимента с помощью
компьютера, т. е. разработке и реализации алгоритма, возвращающего
результаты, аналогичные измеренным данным. В том случае, когда мы
имеем дело с задачей восстановления неизвестной функции по резуль-
татам измерения ее значений, требуется подобрать подходящую функ-
цию, а затем вычислять ее значения и генерировать ошибку с помощью
генератора случайных чисел.
Понятно, что применение методов планирования эксперимента
может дать значительный экономический эффект, но отсутствие соот-
ветствующего оптимального плана может сделать экспериментальную
программу полностью безрезультатной.
Основное внимание в этой работе уделено получению оптимального плана.
Планирование эксперимента предполагает наличие математиче-
ской модели и критерия оптимальности. Сложный характер критериев
требует специальных методов оптимизации. В диссертации рассматри-
ваются два метода случайного поиска глобального экстремума: метод
Метрополиса и ранее изученный метод случайного поиска глобального
экстремума с “памятью”. Оба метода позволяют получать реализации
случайного вектора с плотностью, пропорциональной целевой функции
и далее находить моду рассматриваемой плотности и тем самым полу-
чаем максимум исходной функции.
Магистерская диссертация является продолжением работы над бака-
лаврским дипломом, где находились оптимальные планы для линейной ре-
грессии с использованием случайного поиска.
Настоящая работа прошла апробацию на международных науч-
ных конференциях:
1. III международной конференции “Устойчивость и процессы управле-
ния”, 5-9 октября 2015 г.
2. III International Conference “Stability and Control Processes” in Memory of
V.I.Zubov, 2015.
3. 48 международной научной конференции аспирантов и студентов
“Процессы управления и устойчивость”, 3-6 апреля 2017 г.
✅ Заключение
сии рассмотрена задача построения локально оптимальных планов. Для этого
выбран определенный критерий оптимальности – это критерийD -
оптимальности. Он основан на предположении, что погрешности между ре-
зультатами экспериментов в точках множества планирования и значениями
регрессионной функции в этих же точках множества планирования есть слу-
чайные величины, распределенные нормально.
В этом случае при достаточно большом числе экспериментов оценка
неизвестных параметров нелинейной регрессии по методу наименьших квад-
ратов стремится к истинным параметрам, а дисперсия вектора погрешностей
будет определяться через информационную матрицу. Поэтому объем эллип-
соида рассеяния вектора погрешностей тоже определяется через информаци-
онную матрицу. Уменьшая этот объем, будем уменьшать и величины по-
грешностей для оцененных параметров. Отсюда появляется функция, кото-
рую требуется оптимизировать.
Для нелинейной регрессии эта функция зависит не только от точек
плана, но и от самих параметров. Поэтому задача оптимизации решается при
некоторых параметрах регрессии, которые априори известны. Полученный
план называется локально оптимальным.
Для оптимизации использовались два случайных метода поиска гло-
бального экстремума. Оба метода позволяют находить реализации случайных
векторов, распределенных с плотностью пропорциональной целевой функ-
ции. Поэтому задачу нахождения глобального максимума можно трактовать
как нахождение моды плотности.
Для апробации метода нахождения локально оптимальных планов рас-
сматривалась задача определения радионуклидов в смеси из двух. Рассмот-
рено 9 вариантов смесей радионуклидов.
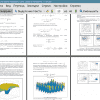
Результат получен двумя способами оптимизации и наглядно представ-
лен рисунком. Легко увидеть промежутки, в которые следует проводить из-
мерения. Они занимают определенный промежуток для каждого измерения.
Особенность в промежутке для последнего измерения заключается в том, что
чем больше разница между полупериодами распада радионуклидов, тем
дальше время последнего измерения.
Таким образом, применение метода планирования эксперимента может
дать значительный экономический эффект, так как получен соответствую-
щий локально оптимальный план.