
Тип работы:	Предмет:	Язык работы:

Математическое моделирование эмиссионной системы с модулятором на основе эллипсоидального полевого катода

Работа №	129977
Тип работы	Магистерская диссертация
Предмет	математическое моделирование
Объем работы	58
Год сдачи	2018
Стоимость	5650 руб.
ПУБЛИКУЕТСЯ ВПЕРВЫЕ
Просмотрено	89

Не подходит работа?

Узнай цену на написание

Содержание

Введение 4
1. Обзор литературы 6
1.1. Эмиссионные системы . . . . . . . . . . . . . . . . . . . . 6
1.2. Используемые методы . . . . . . . . . . . . . . . . . . . . 7
2. Моделирование диодной системы с кусочно-
постоянными граничными условиями на аноде 8
2.1. Физическая постановка задачи для диодной системы . . 8
2.2. Математическая модель диодной системы . . . . . . . . . 9
2.3. Решение граничной задачи для диодной системы . . . . . 10
3. Моделирование триодной системы с нулевыми гранич-
ными условиями на аноде 13
3.1. Физическая постановка задачи для триодной системы с
нулевыми граничными условиями . . . . . . . . . . . . . . 13
3.2. Математическая модель триодной системы с нулевыми
граничными условиями . . . . . . . . . . . . . . . . . . . . 14
3.3. Решение граничной задачи для триодной системы с нуле-
выми граничными условиями . . . . . . . . . . . . . . . . 14
4. Моделирование триодной системы с ненулевыми гра-
ничными условиями на аноде 22
4.1. Физическая постановка задачи для триодной системы . . 22
4.2. Математическая модель триодной системы . . . . . . . . 22
4.3. Решение граничной задачи для триодной системы . . . . 24
5. Моделирование триодной системы методом перекрытия
областей 30
5.1. Физическая постановка задачи для триодной системы на
основе полуэллипсоидального полевого катода . . . . . . 30
5.2. Математическая модель триодной системы на основе по-
луэллипсоидального полевого катода . . . . . . . . . . . . 31
5.3. Решение граничной задачи для триодной системы на ос-
нове полуэллипсоидального полевого катода . . . . . . . 32
5.4. Исследование нулей функций Лежандра . . . . . . . . . . 38
6. Результаты численных расчётов 40
6.1. Расчёт электростатического потенциала . . . . . . . . . . 40
6.2. Расчёт напряжённости . . . . . . . . . . . . . . . . . . . . 42
6.3. Исследование параметров острия . . . . . . . . . . . . . . 48
6.4. Расчёт плотности тока . . . . . . . . . . . . . . . . . . . . 50
6.5. Сравнение методов . . . . . . . . . . . . . . . . . . . . . . 52
Заключение 54
Список литературы 55

Введение

Фото. Robert Williams Wood. 1868-1955.
Благодаря открытию автоэлектронной эмиссии Робертом Вудом в 1897 году, опре-
делилась совершенно новая область микро- и наноэлектроники, а именно вакуумная микро-
электроника [1]. Автоэлектронная эмиссия позволила создать новое поколение эффективных
электронных приборов с высокой эмиссионной способностью. Такие приборы обладают рядом
преимуществ: устойчивость к колебаниям температуры, отсутствие накала, малая чувстви-
тельность к внешней радиации, высокая плотность тока.
Наноразмерные автоэмиссионные системы нашли широкое применение в разработке электронно-лучевых
приборах, а именно, в полевых электронных и сканирующих туннельных
микроскопах. Так же подобные системы представляют собой мини-
атюрные источники рентгеновского излучения, которое используется
для диагностики и внутриполостного лечения онкологических заболеваний [2].
При разработке эмиссионных систем требуется учитывать всё
большее количество геометрических параметров приборов [3]. Задача
является трудоёмкой из-за высокой чувствительности автоэмиссии к
изменению геометрии катода (рис. 0.1). Математическое моделирова-
ние является важным элементом проектирования, который позволяет
предварительно проанализировать возможности новых приборов.
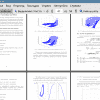
Рис. 0.1. (a) Схематическое изображение диодной системы. Излучение происходит с
острия эмиттера. (b) У излучателя могут быть разные токи эмиссии в зависимости
от геометрии острия, например, (i) круглый наконечник, (ii) тупой наконечник и (iii)
конический наконечник [4].
Цель — разработать математические и физические модели эмиссионных систем с полевым катодом эллипсоидальной формы.
Задачи:
• Рассмотреть физические модели диодной и триодной систем.
• Разработать математическую модель диодной системы.
• Разработать математические модели триодных систем.
• Выбрать методы решения поставленных задач.
• Найти значения электростатического потенциала во всех областях рассматриваемых систем в аналитическом виде.
• Визуализировать полученные результаты для диодной системы.

Возникли сложности?

Нужна помощь преподавателя?

Помощь в написании работ!

ДИПЛОМНЫЕ МАГИСТЕРСКИЕ ДИССЕРТАЦИИ

Курсовые Статьи Диплом Рязань

Заключение

1. В работе представлены физическая и математическая модели ди-
одной системы полевого острия, состоящего из катода и анода
формы полуэллипсоидов вращения.
2. Найдено распределение электрического потенциала в виде разло-
жения по полиномам Лежандра (2.5) для модели диодной системы
с граничными условиями (2.3).
3. Рассмотрены физические и математические модели триодных си-
стем с модулятором на основе острийного полевого катода с ну-
левыми и ненулевыми граничными условиями.
4. Разработаны алгоритмы для нахождения распределения электри-
ческого потенциала для триодных систем с граничными условиями (3.2) и (4.1).
5. Построен алгоритм для нахождения электрического потенциала
для триодной системы с граничными условиями (5.1)–(5.3).
6. Предложены параметры диодной системы с кусочно-постоянными
граничными условиями на аноде.
Данное исследование, посвящённое математическому моделирова-
нию эмиссионных систем с эллипсоидальным катодом, показало необ-
ходимость использования таких специальных функций как полиномы
Лежандра и функции Лежандра. Представление полевого острия в ви-
де эллипсоида вращения даёт возможность использования специаль-
ных координат (координаты вытянутого эллипсоида вращения), кото-
рые упрощают решение задачи.
При решении задач был использован метод разделения перемен-
ных для уравнения Лапласа в координатах вытянутого эллипсоида вра-
щения, метод парных сумматорных уравнений, содержащих полиномы
Лежандра и метод перекрытия областей.

Литература

[1] Фурсей Г. Н. Автоэлектронная эмиссия // Соросовский образова-
тельный журнал. 2000. Т. 6. No 11. C. 96–103.
[2] Трубецков Д. И., Краснова Г. М. О современном состоянии сверх-
высокочастотных вакуумных электронных и микроэлектронных
приборов с управляемой эмиссией // Изв. вузов «ПНД». 2013.
Т. 21. No 1. C. 35–66.
[3] Елинсон М. И., Васильев Г. Ф. Автоэлектронная эмиссия. М.: Физ-
матлит, 1958. 272 с.
[4] Xiaosheng Fang, Yoshio Bando, Ujjal K. Gautam, Changhui Ye and
Dmitri Golberg. Inorganic semiconductor nanostructures and their
field-emission applications. The Royal Society of Chemistry, vol. 18,
2008, pp. 509–522.
[5] Гусинский Г. М., Баранова Л. А., Найденов В. О. Субмикронный
источник свободных электронов // Журнал технической физики.
2015. Т. 85. Вып. 3. C. 129–132.
[6] T. A. Roth. The field emitter: Electric field calculation // Journal of
Applied Physics, vol. 45, No. 11, November 1974, pp. 4771–4773.
[7] Виноградова Е. М., Егоров Н. В. Математическое моделирование
диодной системы на основе полевого эмиттера // Журнал техни-
ческой физики. 2011. Т. 81. Вып. 9. C. 1–5.
[8] Виноградова Е. М., Листрукова А. В. Математическое моделирова-
ние квадрупольной электростатической линзы // Вестник Санкт-
Петербургского университета. Серия 10: Прикладная математика.
Информатика. Процессы управления. 2016. No 1. С. 19–27.
[9] Калатурская Э. В., Виноградова Е. М. Расчёт полевого диода ци-
линдрической формы // Процессы управления и устойчивость.
2017. Т. 4. No 1. С. 91–94.
[10] Гобсон Е. В. Теория сферических и эллипсоидальных функций.
М.: ИЛ, 1952. 476 с.
[11] Тихонов А. Н., Самарский А. А. Уравнения математической физи-
ки. М.: Наука, 1977. 736 с.
[12] Уфлянд Я. С. Метод парных уравнений в задачах математической
физики. Л.: Наука, 1977. 220 с.
[13] Виноградова Е. М. Математическое моделирование электронно-
оптических систем. Учебно-метод. пособие. — СПб., 2005. — 112 с.
[14] Маслова Т. А., Виноградова Е. М. Моделирование эллиптического
диода // Процессы управления и устойчивость. 2016. Т. 3. No 1. С. 194-198.
[15] T. A. Maslova and E. M. Vinogradova, ”Diode System on the Basis of
Field Emitter with Semi-Ellipsoid Shape Mathematical Modeling”, in
Young Researchers in Vacuum Micro/Nano Electronics (VMNE-YR),
Saint Petersburg, Oct. 2016.
...