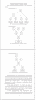Тема: Модели конкуренции и кооперации многоуровневых сетей поставок

Операционное и промышленное моделирование, а также операционный менеджмент имеют давнюю историю, уходящую корнями к первой промышленной революции. Планирование производства, управление запасами, проектный менеджмент, контрольные диаграммы, статистические отчеты, опросники удовлетворенности клиентов, ранжирование и бенчмаркинг - вот лишь некоторые из инструментов, уже довольно давно используемых для улучшения операционной и промышленной деятельности. Но вместе с тем, как росли масштаб и сложность цепочек поставок, существенно усложнялись логистические и операционные проблемы, и традиционные инструменты, в свою очередь, уже не могли покрыть весь спектр возникающих задач. Это привело к необходимости разработки новых методов управления, а также более комплексных подходов к моделированию: все чаще ощущалась потребность в комбинировании инструментария математического моделирования и экономических реалий в сфере сетей поставок, действующих в глобальном масштабе.
Сегодня сети поставок являются неотъемлемым компонентом торговых отношений и оказывают огромное влияние на корпоративные выживаемость и развитие. Именно поэтому плохо реализованная операционная деятельность чаще всего приводит к значительным убыткам и нереализованной прибыли. Таким образом, принимая во внимание этот факт, а также увеличившуюся сложность структуры сетей поставок, глобализацию и возможность кооперации, можно заключить, что исследование вопросов конкуренции и кооперации в сетях поставок является очень актуальной задачей.
Целью данной работы является моделирование многоуровневых сетей поставок дистрибутивного типа, изучение моделей конкуренции и кооперации в сетях поставок, нахождение решений и сравнение результатов моделирования на кейсах реальных компаний. В работе исследованы несколько структур сетей поставок. Первая глава диссертации посвящена сетям поставок с древовидной структурой. Во второй главе проанализированы сети со сборочной и дистрибутивной структурами. Каждая из перечисленных моделей математически формализуется с помощью иерархической игры специального вида, для которой строится равновесное решение Нэша в условиях конкуренции между участниками сети поставок. Для каждой из рассмотренных структур вычисляется кооперативное решение в форме взвешенного арбитражного решения Нэша, где в качестве точки статус-кво рассматривается равновесное решение. Для каждой из структур сетей поставок приводится численный пример сети поставок, на котором иллюстрируются алгоритмы построения решений, и проводится сравнение результатов моделирования.
В третьей главе данной работы приведены результаты применения разработанной методологии анализа сетей поставок для прикладных задач. В первом параграфе анализируется сеть поставок компании Х - производителя целлюлозно-бумажной продукции, во втором - сеть поставок дистрибьютора У электро-технических товаров и комплектующих. В заключение приведены выводы по результатам работы и список использованной литературы.
Обзор литературы
Сети поставок встречаются во всех сферах торговли и бизнеса, и этот факт делает их одним из самых популярных объектов изучения многих экономистов и ученых. Впервые ввела такое понятие как менеджмент сетей поставок, а также рассмотрела задачу управления цепочками поставок как концепцию, заключающуюся в интегрированном подходе к планированию и управлению услугами информационными и товарными потоками, аналитик консалтинговой компании «Буз Аллен Гамильтон» Кейт Оливер [8] в 1982 году. Концепция была быстро принята и получила широкое распространение и развитие.
Первые работы по менеджменту сетей поставок были посвящены изучению децентрализованных моделей, т.е. таких сетей поставок, в которых участники действуют независимо друг от друга. Примером таких работ могут служить статьи Зисса С. [14], Викерса Д. [11] и Тьяги Р. К. [10].
Позднее ученых заинтересовала кооперация участников сети и управление рисками. Кахон Г.П. [3] в своих работах исследовал вопрос влияния координирующих контрактов, а Кайя М. и Озер О. [7] -
контрактирование сети для дележа рисков, прибыли и информации. Одновременно с темой кооперации также продолжало развиваться направление, связанное с изучением конкуренции в децентрализованной модели сети поставок. Например, работа Адиды Е. и ДеМигеля В. [1] посвящена вопросами конкуренции с уклоном в исследование влияния дифференциации товаров и потребителей.
Моделирование многоуровневых сетей поставок началось относительно недавно. Пионерами этой темы были Корбетт Ч. и Кармаркар У. [6], смоделировав конкуренцию в многоуровневых сетях с заданным спросом. Позже, Карр С. в соавторстве с Кармаркаром У. [4] опубликовали работу, в которой была исследована модель конкуренции в многоуровневой сети поставок со сборочной структурой. Одними из последних работ,
посвященных моделированию многоуровневых сетей поставок, являются исследование Чо С.-Х. [5], изучающее горизонтальную кооперацию в
многоуровневых сетях поставок, и статья Жоу Д., Кармаркара У. и Джанга Б. [13], которая является обобщением работы [4] на случай дистрибутивной структуры сети поставок и изучает вопросы координации
децентрализованной сети, влияния изменения концентрации участников и вида функции спроса.
Модели сетей поставок, исследованные в данной работе, основаны на модели Жоу Д., Кармаркара У. и Джанга Б. [13], которая обобщена на случай произвольных фирм, и модели Карра С. и Кармаркара У. [4], которая также обобщена на случай произвольных фирм. В работе обе модели [4] и [13] обобщены на случай произвольной дистрибутивной сети поставок. Кроме того, результаты исследования вопросов конкуренции и кооперации в многоуровневых сетях поставок опубликованы в статье [12], а результаты анализа практических кейсов компаний опубликованы в работах [9] и [2].

Купить

В рамках данной работы нами были рассмотрены модели конкуренции и кооперации в многоуровневых сетях поставок с различной дистрибутивной структурой.
В первую очередь нами были исследованы сети поставок с древовидной структурой. Данный тип сетей поставок был математически формализован с помощью иерархической игры на древовидном графе, на основе которой была построена математическая модель многоуровневой сети поставок с древовидной структурой. Для построенной математической модели было предложено два алгоритма нахождения объемов производства и цен всех участников сети поставок, каждый из которых соответствует одной из моделей взаимодействия участников: конкуренция и кооперация. В условиях конкуренции, т.е. когда каждый из участников действует независимо от других, преследуя лишь личные выгоды, нами предложен алгоритм нахождения абсолютного равновесия по Нэшу, обеспечивающий максимальный выигрыш каждому участнику. Кроме того, данный алгоритм при конкретизации графа сети поставок позволяет построить решение в аналитическом виде. В кооперативной модели, т.е. когда все участники образуют максимальную коалицию, преследуя цель максимизировать общую прибыль, в качестве решения было предложено взвешенное арбитражное решение Нэша, для нахождения которого сформулирована задача нелинейного программирования с нелинейными ограничениями. Для иллюстрации алгоритмов построения решений приведен численный пример древовидной сети поставок, на котором также проводится сравнение результатов моделирования.
Далее в рамках данной работы была рассмотрена проблема нахождения децентрализованного (конкурентного) и централизованного
(кооперативного) решений в дистрибутивных сетях со сборочной и дистрибутивной структурами. Прежде всего, сети поставок данных типов были математически формализованы с помощью иерархической игры на графе соответствующей структуры. Нами предложены алгоритм нахождения равновесного по Нэшу решения при конкуренции между участниками сети и способ нахождения кооперативного решения в смысле взвешенного арбитражного решения Нэша. Для наглядной демонстрации алгоритмов построения указанных решений в дистрибутивных сетях в конце второй главы рассмотрен численный пример сети поставок с дистрибутивной структурой, на котором также проведено сравнение результатов численного моделирования.
В третьей главе диссертации приводятся результаты применения разработанной методологии анализа дистрибутивных сетей поставок на кейсах реальных компаний. В первом кейсе проведен анализ древовидной сети поставок на основе данных компании Х - крупного производителя целлюлозно-бумажной продукции. На основе предоставленных данных построена древовидная сеть, найдены равновесное и кооперативное решения, и проведен сравнительный анализ результатов моделирования. Во втором кейсе разработанная методология опробована на данных дистрибьютора У электротехнических товаров и комплектующих. После анализа структуры поставок дистрибьютора У, была построена дистрибутивная сеть поставок, найдены равновесное и кооперативное решения, проведен сравнительный анализ результатов численного моделирования.
Купить