Всё чаще квантовые и математические методы в современном мире применяются к различным областям знаний, в частности к медицине [15, 57]. Важную роль на текущий момент завоевывает квантовая физика при лечении доброкачественных и злокачественных опухолей. Каждый случай является при лечении уникальным, и при обобщении для решения круга данных задач, необходимо учитывать различные факторы.
Применение пучков заряженных частиц в медицине для удаления опухолей имеет огромное значение и практическое применение. Однако для получения качественного результата на выходе необходимо подобрать наиболее подходящий алгоритм для оптимизации динамики частиц пучка [5, 43, 76, 82]. Качество оптимизации пучка можно оценивать по многим параметрам, и чаще всего из-за сложности физического процесса и количества вовлеченных в него частиц, нельзя выбрать только один конкретный параметр, который бы полностью характеризовал «качество» динамики пучка заряженных частиц. Исходя из этих соображений были выбраны такие характеристики динамики пучка, как однородность пучка по фазам входящих в пучок частиц, по энергиям этих частиц, а также по доле частиц, дошедших до конца ускорителя и находящихся в режиме ускорения [36, 45].
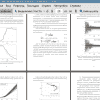
В качестве математической модели для описания динамики пучка был выбрана хорошо зарекомендовавшая себя математическая модель интенсивного пучка в поле бегущей волны в рамках линейного волноводного ускорителя [8, 62, 63].
В связи с тем, что у нас присутствуют несколько критериев оптимизации не представляется возможным применение классических методов оптимизации одного критерия качества динамики, поэтому имеет смысл применить стохастические методы оптимизации для задач динамики пучка заряженных частиц. Подобные методы доказали свою эффективность в ряде подобных задач, где присутствуют несколько разнородных критериев оптимизации [34, 46, 52]. В частности, в данной работе будут рассмотрены метод роя частиц и генетические алгоритмы глобальной и многокритериальной оптимизации. Стохастические методы наиболее подходят к применению для текущих задач, т.к. размерность задач достаточно велика, поэтому найти аналитически градиент критерия качества не представляется возможным. К тому же критерий качества обладает множеством локальных минимумов, а стохастические методы имеют возможность преодолевать локальные минимумы для достижения глобального минимума [83].
Целью данного исследования является сравнение стохастических методов оптимизации для задач динамики пучка заряженных частиц. Также итогом данного исследования станет моделирование и оптимизация примера интенсивного пучка.
Для решения поставленной цели будут решены следующие задачи:
• изучение информационной базы по тематике исследования,
• выделение подходящих направлений и методов,
• применение выбранных методов к заданной математической модели динамики заряженных частиц пучка,
• сравнение результатов выбранных методов.
В данной работе была рассмотрена проблема моделирования и оптимизации динамики интенсивного пучка в поле бегущей волны с помощью трех различных методов оптимизации: метода роя частиц, генетического алгоритма глобальной оптимизации и генетического алгоритма многокритериальной оптимизации. Данные методы были реализованы в среде и на языке Matlab [20].
При этом решены следующие задачи:
• в процессе исследования была изучена информационная база, включающая в себя текущее состояние дел в рамках научного исследования, изучены стохастические методы оптимизации для задач динамики пучка заряженных частиц,
• в качестве наиболее подходящих для дальнейшего исследования и применения были выбраны методы роя частиц, генетический алгоритм глобальной оптимизации и генетический алгоритм многокритериальной оптимизации,
• применение выбранных методов к заданной математической модели динамики заряженных частиц пучка в поле бегущей волны было осуществлено на практике численно. Полученные результаты представлены в работе. Также было проведено сравнение результатов и описан процесс получения итоговых данных.
В дальнейшем предполагается:
• сравнить методы для большего набора данных [16, 37];
• применить полученные данные на другой модели ускорителя заряженных частиц;
• добавить в расчеты поле Кулона [12];
• применить метод матричного формализма для большого количества частиц [1, 19].
Помощь студентам и аспирантам в выполнении работ от наших партнеров
