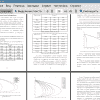
Тема: АНАЛИЗ СТАЦИОНАРНЫХ РЕШЕНИЙ УРАВНЕНИЙ ОДНОМЕРНЫХ МОДЕЛЕЙ ГЕМОДИНАМИКИ
Закажите новую по вашим требованиям
Представленный материал является образцом учебного исследования, примером структуры и содержания учебного исследования по заявленной теме. Размещён исключительно в информационных и ознакомительных целях.
Workspay.ru оказывает информационные услуги по сбору, обработке и структурированию материалов в соответствии с требованиями заказчика.
Размещение материала не означает публикацию произведения впервые и не предполагает передачу исключительных авторских прав третьим лицам.
Материал не предназначен для дословной сдачи в образовательные организации и требует самостоятельной переработки с соблюдением законодательства Российской Федерации об авторском праве и принципов академической добросовестности.
Авторские права на исходные материалы принадлежат их законным правообладателям. В случае возникновения вопросов, связанных с размещённым материалом, просим направить обращение через форму обратной связи.
📋 Содержание
Глава 1. Обзор литературы 5
1.1. Объект исследования 5
1.2. Математическая модель 5
Глава 2. Получение стационарных решений уравнений одномерной гемодинамики 12
2.1. Постановка задачи 12
2.2. Получение стационарных решений 14
2.3. Результаты и выводы 17
Глава 3. Вычислительные эксперименты 19
3.1. Случай сосуда постоянного сечения 21
3.2. Случай сосуда с переменным сечением 29
3.3. Результаты и выводы 39
Заключение 41
Список литературы 42
📖 Введение
Математическое моделирование является важным для современной медицины, так как на основе моделей можно прогнозировать последствия хирургических операций, оптимизировать форму имплантов, исследовать их влияние на особенности течения крови [6]. Для моделирования кровотока в больших сосудистых системах принято рассматривать одномерные модели, полученные осреднением трехмерных уравнений гидродинамики. Такие модели, с одной стороны, удобны для практической реализации, а с другой стороны, позволяют получать результаты, хорошо согласующиеся с результатами эксперимента [7] и результатами расчетов по трехмерным моделям [8].
Настоящая работа посвящена одномерным моделям течения крови, в рамках которых учитывается такое наблюдаемое свойство крови, как неньютоновость. В работе получены стационарные решения для случаев разных реологических моделей крови как жидкости. Для ряда моделей удалось получить интегралы нелинейных уравнений, для остальных моделей решения были получены численно. Отдельно рассмотрен случай сосудов с наличием локального сужения.
Целью работы являлось нахождение и анализ стационарных решений уравнений одномерной гемодинамики.
Для достижения этой цели предстояло решить ряд задач:
1. Постановить задачи о нахождении стационарных решений.
2. Найти первые интегралы для случаев конкретных неньютоновских моделей.
3. Разработать программы, реализующие алгоритмы численных методов нахождения стационарных решений .
4. Провести численные расчеты в случае сосудов с постоянным и переменным сечением.
Работа состоит из трех глав. В главе 1 проведен обзор литературы. В качестве объекта исследования рассматривается кровь, её состав, роль и функции. Также в главе 1 дано описание общей математической течения крови как течения вязкой несжимаемой жидкости. Вводятся предположения, необходимые для получения одномерной модели и представлены основные уравнения. Глава 2 посвящена нахождению стационарных решений уравнений одномерной гемодинамики. Произведена постановка задачи о нахождении стационарных решений, описываются случаи моделей, для которых возможно получение интегралов. Отдельно описываются алгоритмы проведения расчетов для случаев, когда можно найти интегралы и для случаев, когда этого сделать не удается. В главе 3 представлены результаты вычислительных экспериментов. Рассматриваются случаи сосудов с постоянным и переменным поперечным сечением. В заключении представлены основные результаты и выводы.
✅ Заключение
1. Поставлены задачи о нахождении стационарных решений уравнений одномерной гемодинамики.
2. Для ряда моделей получены первые интегралы.
3. Разработано программное обеспечение, реализующее алгоритмы численных методов для нахождения стационарных решений.
4. Получены и проанализированы стационарные решения.
По полученным результатам можно сделать следующие выводы:
1. Показано, что для всех рассмотренных моделей уплощение профиля скорости, характерное для крови, приводит к уменьшению промежутка существования стационарного решения.
2. Показано, что увеличение гематокрита тоже приводит к уменьшению промежутка существования стационарного решения.
3. Показано, что при уменьшении ширины бляшки и ее высоты наблюдается увеличение промежутка существования стационарного решения.