Введение 4
1. Постановка задачи 8
2. Модель робота и предположения 10
3. Закон управления 14
4. Основной результат 18
5. Доказательства 21
6. Результаты компьютерного моделирования 30
7. Заключение 43
Список литературы 44
Купить

За последние десятилетия тема управления группой мобильных роботов и их фор­мацией стала широко изучаемой [1, 2]. В данной области неуклонно растёт интерес к теме децентрализованного распределённого управления в условиях сенсорных ограни­чений и отсутствия коммуникации между роботами.
В работе рассматривается специальная задача децентрализованного и распреде­ленного управления формацией группы роботов для обеспечения эффективного заме­тающего покрытия территории. Возникающая область задач заметающего покрытия группой роботов быстро приобретает всё большее значение благодаря постоянно расту­щему использованию мобильных роботизированных групп и беспроводных сетей для исследования или распределенной обработки протяженных объектов.
Примеры соответствующих миссий включают автоматическое разминирование [3], экологические исследования, разведку, очистку корпуса корабля, мониторинг мест за­хоронения отходов на дне океана [4], съемку морского дна для разведки углеводородов. [5], обнаружение источников утечки опасных химических веществ, выброса паров или загрязняющих веществ, обнаружение разливов нефти, поиск экстремумов естественных полей [6], спасательные операции в городах после стихийных бедствий или техногенных катастроф, а также многое другое.
Чтобы добиться успеха в таких миссиях, элементы сети должны занимать пра­вильные, желательно оптимальные, места с минимальным требованием, чтобы любая точка рабочего пространства была покрыта зоной видимости какого-то элемента. Если сеть большая, размещение элементов в таких местах внешними средствами может быть сложным и дорогостоящим. Это делает автономное саморазвертывание мобильных эле­ментов привлекательным вариантом [7, 8, 9, 10]: начиная со случайных позиций, ро­боты должны сами достичь оптимального развертывания за счет скоординированных действий. Для достижения этой цели необходимы масштабируемые и распределенные законы управления, сочетающие в себе простоту реализации, малое потребление ресур­сов, устойчивость к отказам элементов, их взаимозаменяемость и твердые гарантии глобальной сходимости.
Однако многочисленные исследования задачи покрытия были сосредоточены в ос­новном на геометрических аспектах проблемы [11, 12, 13]. Среди наиболее популярных тем — задача размещения узлов (сколько узлов нужно в сети и где их разместить) и построения пути, проходящего в непосредственной близости от любой точки интересу­ющей области. При этом мало внимания уделялось вопросу автономного самораспреде- ления групп роботов.
В частности, в задаче рассылки узлов основное внимание уделяется распределению узлов по предварительно вычисленным точкам, определенным алгоритмом размеще­ния, и, возможно, улучшению качества покрытия; см., например, [14, 15]. Многоагент­ное управление движением для достижения заданной статической конфигурации — еще одна хорошо изученная область; см., например, [16, 17]. Некоторые из соответствующих подходов, например, основанные на потенциальных полях, виртуальных силах [18, 19] или разбиении Вороного [17, 20], способны работать с неизвестными рабочими зонами. В то же время доказательные гарантии глобальной сходимости по-прежнему остают­ся редкостью в соответствующей литературе, а проверка алгоритма часто сводится к компьютерным тестам и/или вторичным теоретическим фактам, таким как локальная оптимальность, вытекающая из сходимости к центрам ячеек Вороного. Доступно лишь несколько строгих результатов по глобальной сходимости (см., например, [21, 22, 23]), а разработка строго обоснованных глобально сходящихся законов управления для задач покрытия группой роботов в целом находится на ранней стадии.
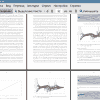
Предложенный в работе строго обоснованный и глобально сходящийся распреде­ленный закон управления для задачи покрытия, сочетающий элементы барьерного и заметающего покрытия [24], призван заполнить некоторые из вышеперечисленных про­белов. Группа роботов неизвестного размера должна прийти к общему перпендикуляр­ному сечению неизвестного коридора, равномерно распределиться по его ширине в мак­симально плотный сете-образный барьер и прочесать коридор, двигаясь по нему как единое целое с предварительно заданной скоростью в заданном направлении. Эта схе­ма покрытия представляет интерес для различных приложений, включая разминирова­ние, экологические исследования, разведку при спасательных операциях и мониторинг экологических границ, и это лишь некоторые из них.
Для описанной выше миссии алгоритмы распределенного управления с гарантиями глобальной сходимости приведены в [25, 22, 23]. Однако соответствующие результаты сильно зависят от предположения, что коридор не содержит препятствий. С одной сто­роны, это предположение не выполняется для многих реальных приложений. С другой стороны, наличие препятствий существенно усложняет дело, делает невозможным ба­зовые алгоритмические решения из [25, 22, 23] и добавляет дополнительную существен­ную проблему обхода препятствий к набору задач, решаемых распределенным образом, так что основная цель миссии должна быть выполнена при наличии препятствий.
Кроме того, выводы [25, 22] связаны с моделями дискретного времени и существен­но опираются на ограниченность снизу периода дискретизации по времени. Это ограни­чение может препятствовать своевременному обновлению управления и, таким образом, может повлечь за собой негативное влияние на работу команды, например, привести к столкновению роботов друг с другом, эта проблема не проработана в [25, 22].
В данной квалификационной работе рассматриваются мобильные роботы, переме­щающиеся с ограниченной скоростью, и смоделированные как простые интеграторы, каждый из которых имеет конечную зону видимости. В качестве рабочей зоны рас­сматривается коридор, который моделируется как полоса между двумя параллельными линиями в теоретической части статьи. Роботы не знают размера команды и ширины коридора и не могут различать друг друга, играть разные роли в команде и не оснаще­ны средствами связи.
Предлагается простой закон управления, который индивидуально и независимо выполняется каждым роботом, является общим для всех, выстраивает роботов в мак­симально плотную сеть-барьер поперек коридора, а также перемещает этот барьер по коридору с заданной скоростью в заданном направлении. Кроме того, этот закон исклю­чает столкновения роботов друг с другом, препятствиями и стенами коридора. При прохождении полосы препятствий равномерность распределения по коридору обяза­тельно нарушается, однако предложенный закон продолжает поддерживать требуемую скорость движения вдоль коридора и расположение всех роботов на общем поперечном (подвижном) сечении коридора. При этом равномерность распределения автоматически восстанавливается после полного преодоления полосы препятствий. Это строго обосно­вано доказательством глобальной сходимости и подтверждено тестами компьютерного моделирования.
Текст работы организован следующим образом. Раздел 1 описывает проблему. Раз­дел 2 содержит необходимые условия для достижимости поставленной цели управления. Закон управления и связанные с ним определения и предположения представлены в раз­деле 3, а основные результаты в разделе 4. Все доказательства вынесены в раздел 5. Раздел 6 приводит результаты компьютерной симуляции. Раздел 7 содержит краткие выводы.
Купить