РЕГУЛЯРИЗОВАННОЕ АСИМПТОТИЧЕСКОЕ РЕШЕНИЕ ЗАДАЧИ КОШИ ДЛЯ НЕОДНОРОДНОГО УРАВНЕНИЯ ШРЕДИНГЕРА В КВАЗИКЛАССИЧЕСКОМ ПРИБЛИЖЕНИИ В ПРИСУТСТВИИ «СИЛЬНОЙ» ТОЧКИ ПОВОРОТА У ПРЕДЕЛЬНОГО ОПЕРАТОРА
Сингулярно возмущенные задачи для дифференциальных и интегро- дифференциальных уравнений с нарушенными условиями стабильности спектра предельного оператора уже давно хорошо известны специалистам в математической и теоретической физике. Особый интерес среди таких задач вызывают те, в которых спектральные особенности выражены в виде точечной нестабильности (см., например, [1]-[3]). В работах посвященных сингулярно возмущенным задачам некоторая часть особенностей такого вида названа точками поворота и проведена их классификация:
1) простая точка поворота — собственные значения предельного оператора изолированы друг от друга и одно собственное значение в отдельных точках обращается в нуль (см.[2], [4], [5]);
2) слабая точка поворота — хотя бы пара собственных значений пересекаются в отдельных точках, но при этом предельный оператор сохраняет диагональную структуру вплоть до точек пересечения, а базис из собственных векторов сохраняет гладкость (см. [6], [7]);
3) сильная точка поворота — хотя бы пара собственных значений пересекаются в отдельных точках, но при этом предельный оператор меняет диагональную структуру на жорданову в точках пересечения,а базис собственных векторов теряет гладкость (см. [8]).
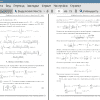
В настоящей работе рассматривается нестационарное и неоднородное уравнение Шредингера с гамильтонианом H(p x) = p2 + X, которое при ква- зиклассическом переходе порождает сингулярно возмущенную задачу Коши с «сильной» точкой поворота. Отметим, что задача для однородного и стационарного уравнения с таким профилем потенциальной энергии является одной из немногих точно решаемых проблем квантовой механики (см.[9], §24).
Кратко обозначим здесь суть квазиклассического приближения в квантовой механике. Основное уравнение теории — уравнение Шредингера — при записи в координатном представлении является уравнением в частных производных второго порядка по координатам и первого порядка по времени и содержит постоянную Планка ~. Точные решения этого уравнения удаётся отыскать только для небольшого числа простейших случаев, реальные задачи значительно сложнее и точных решений получить для них не удаётся. Однако для широкого спектра задач может оказаться правильным считать ~ малой величиной и пытаться искать приближенные (по малому ~) решения (см.[9], Гл. 7). Строго говоря, постоянная Планка ~ является размерной величиной и имеет вполне конкретное значение, и утверждение о малости ~ следует пониматв в том смысле, что всегда можно выделить безразмерную комбинацию параметров, содержащую ~ в какой-то степени, малую по сравнению с другими безразмернвхми параметрами, не содержащими ~.
При описанном ввппе квазиклассичком переходе возникают различного рода сингулярно возмущеннвхе задачи для уравнения Шрёдингера, в том числе задачи с точками поворота. Перввхе существеннвхе резулвтатвх асимптотического интегрирования задач с классическими точками поворота (в нашей классификации они относятся к третвему типу) бвхли полученвх в годвх создания квантовой механики (Г. Вентцелв, X. Крамере, Л. Бриллюэн, 1926 год) — метод В КБ. В далвнейшем бурное развитие получил метод канонического оператора В.П. Маслова и его различнвхе модификации , удалосв обобщитв применяемвхе подходах на другие сингулярно возмущенные задачи, а не только квантомеханические (см., например,[10]—[14]).
В настоящей статье развивается другой общеизвестный подход к решению сингулярно возмущенных задач — метод регуляризации С.А. Ломова. В условиях стабильного спектра предельного оператора метод регуляризации хорошо разработан и успешно применяется [15]. Для сингулярно возмущенных задач с нестабильным спектром законченной математической теории до сих пор нет, хотя с общематематических позиций их стали изучать порядка 50 лет назад. Построение регуляризованной асимптотики решения одной из таких задач, а именно задачи со спектральной особенностью в виде сильной точки поворота, является основной целью данной работы. Во многом наши исследования по асимтотическому интегрированию задачи Коши для нестационарного и неоднородного уравнения Шредингера с обозначенным выше гамильтонианом при ~ ! 0 представляют собой развитие идей работы [8], где рассмотрена задача Коши для параболического уравнения с сильной точкой поворота. В дальнейшем везде в работе будем использовать обозначение " вместо ~ что является более естественным в теории сингулярных возмущений.
При выполнении условий стабилвности спектра пределвного оператора, как уже было отмечено во введение, метод регуляризации С.А. Ломова дает достаточно простой рецепт поиска регуляризирующих функций. В случае спектральных особенностей у пределвного оператора построения сложнее. В предложенной работе регуляризирущие функции, описвхвающие нерегулярную зависимости решения от малого параметра, и регуляризирующий оператор, связанный с точечной необратимостью предельного оператора, успешно найдены для задачи со спектральной особенностью в виде сильной точки поворота, и тем самым основная проблема метода регуляризации успешно решена, что подтверждается результатами наших исследований.
