В работе рассматривается новый подход моделирования несжимаемых жидкостей - дым Шредингера. С его помощью можно визуализировать созданную модель.
В компьютерной графике симуляция потока жидкости или газа является одной из наиболее любопытных и актуальных задач, ведь ее перед собой ставят специалисты в различных сферах деятельности - ученые, разработчики компьютерных игр, мультипликаторы.
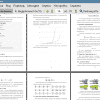
Изначально в компьютерной графике разработка симуляций жидкостей была исключительно для научных целей. Например, моделирование атмосферных явлений (рис.1). Это стало возможно благодаря методам вычислительной гидродинамики. И несмотря на то, что сейчас более популярней становятся другие отрасли применения симуляции жидкости, использование средств вычислительной гидродинамики в научных целях не теряет своей актуальности в компьютерной графике. Интересно то, что порой модели, созданные в научных целях, не уступают в своей зрелищности и реалистичности симуляциям, использующиеся в коммерческих целях.
Рисунок 1. Моделирование атмосферных явлений по данным за октябрь 1979 г.
Наиболее популярным применением моделирования потока жидкостей являются спецэффекты в фильмах. Такие симуляции обычно требуют высокоточных вычислений и выглядят реалистично. На рис.2 представлена такая модель.
Рисунок 2. Компьютерное моделирование воды в фильме Оз: Великий и Могучий. Картинка сверху - как снималось на самом деле. Картинка снизу - что сделали с помощь. компьютерной графики.
Не меньшей популярностью симуляция жидкостей пользуется в мультфильмах и компьютерных играх. И если в мультфильмах художники нередко стремятся создать реалистичные модели (рис.3), вычисления которых зачастую занимают часы и даже месяцы, то в компьютерных играх используются менее точные вычисления, которые производятся в режиме реального времени (рис. 4).
Рисунок 3. Реализация воды в мультфильме Моана.
Рисунок 4. Реализация воды в компьютерной игре The Elder Scrolls V: Skyrim
При моделировании потока жидкости стоит учитывать несколько важных факторов. Пожалуй, одним из самых значимых условий является возможность отобразить некоторые физические характеристики потока в компьютерной модели, например, плотность, скорость, сжимаемость/несжимаемость, давление, теплопроводность и температура. Также возможность добавлять в модель объекты, мешающие движению потоку (различные препятствия), и конечно же симуляция взаимодействия двух жидкостей.
В зависимости от поставленной задачи, может отдавать предпочтения различным типам моделей. Например, сеточные методы подходят для симуляции гладкой водной поверхности как нельзя лучше. А в методах с использованием частиц не возникнет трудностей с соблюдением закона сохранения массы (или эти проблемы можно решить путем небольших модификаций), и обычно работают быстрее сеточных симуляций.
В последние годы популярность стали набирать так называемые смешанные методы, которые использует подходящие для решения задачи преимущества одной из групп методов. Однако гибридные методы требуют больших вычислительных затрат, которые не всегда себя оправдывают.
Разработчики модели сталкиваются с такой сложной проблемой как поиск компромисса между реалистичностью симуляции и разумным использованием имеющихся вычислительных ресурсов. Для построения точной и реалистичной модели, как правило, используются суперкомпьютеры с большим объемом оперативной памяти и видеопамяти.
Рассматриваемый в данной работе алгоритм, называющийся дымом Шредингера, был разработан и представлен на конференции SIGGRAPH в 2016 году [1]. Он позволяет преодолевать традиционно возникающие проблемы в частях алгоритма, связанных с завихренностью и адвекцией потока. В то же время, по словам авторов этого метода, он дает реалистичные результаты, является стабильным и относительно несложным в реализации, при этом не требуя большого количества вычислительных ресурсов. Но у него есть некоторые недостатки.
Хоть алгоритм и не требует больших вычислительных ресурсов, некоторые из его частей являются ресурсозатратными (например, быстрое преобразование Фурье). Из-за этого увеличивается время на вычисления модели.
В рамках данной магистратской диссертации была поставлена цель адаптировать модель дыма Шредингера для вычислений на массивно-параллельных архитектурах, в которой также будет учитываться вязкость используемых веществ.
Для достижения данной цели нужно было решить следующие задачи:
1. Изучить алгоритм несжимаемого потока Шредингера и оптимизировать его с помощью объекто - ориентированного языка программирования C#.
2. Найти теоретическое обоснование добавления параметра вязкости вещества в существующую модель.
3. Перенести полученный код на GPU с использованием библиотеки ускоренных вычислений ArrayFire, которая позволяет запускать приложения на CUDA или OpenCL для параллельных вычислений.
4. Провести ряд тестов на производительность полученного кода.
Работа структурирована следующим образом:
• В первой главе рассказывается о подходите моделирования несжимаемый жидкостей, описывается его исходный алгоритм.
• Вторая глава посвящена обоснованию параметра вязкости, который можно добавить в реализованную модель.
• В третьей главе более подробно рассказывается о переносе алгоритма дыма Шредингера. Также представлены результаты ряда тестирований производительности к реализованного кода.
• В заключении представлены выводы про проделанной работе.
Все следующие задачи были реализованы:
1. Изучить алгоритм несжимаемого потока Шредингера и оптимизировать его с помощью объекто-ориентированного языка программирования C#.
2. Найти теоретическое обоснование добавления параметра вязкости вещества в существующую модель.
3. Перенести полученный код на GPU с использованием библиотеки ускоренных вычислений ArrayFire, которая позволяет запускать приложения на CUDA или OpenCL для параллельных вычислений.
4. Провести ряд тестов на производительность полученного кода.
