1 Введение 2
1.1 Решение Шварцшильда 2
1.2 Вечные черные дыры и мотивировка задачи о коллапсе 2
1.3 Подход к гравитации в форме теории вложения 3
2 Описание коллапса в сопутствующей системе отсчета 4
2.1 Сопутствующие координаты и общие уравнения гравитационного поля с пы­левидной материей 4
2.2 Решение внутренней задачи для однородного шара 7
2.3 Выбор параметров для решения внешней задачи 8
2.4 Попытка гладкого сшивания метрики на границе пылевидного шара 9
2.5 Условия Израэля 10
2.6 Построение вложения для коллапса однородного шара с начальным радиусом, совпадающим с радиусом Шварцшильда 12
2.6.1 Вложение закрытой модели Фридмана 13
2.6.2 Вложение Фронсдала для геометрии Шварцшильда 13
2.6.3 Поверхность сшивки 14
2.6.4 Конечные формулы вложения 16
2.7 Построение вложения для коллапса однородногоо шара с произвольным на­чальным радиусом 19
2.7.1 Сшивка вложения Фридмана с семимерной модификацией Фронсдала 19
2.7.2 Конечные формулы вложения 20
3 Построение коллапса однородного пылевидного шара без сшивания реше­ний 22
3.1 Непрерывная метрика для коллапса однородного шара 23
3.2 Построение вложения непрерывной метрики и конечные формулы 23
4 Заключение 25
A Приложения 25
A.1 Обращение параметрической зависимости, функция y(x) 25
Список литературы 26
Купить

1.1 Решение Шварцшильда
В 1916 году Карлом Шварцшильдом было найдено точное решение вакуумных уравнений Эйнштейна в отсутствии Л-члена и в предположении о наличии сферической симметрии [1]
(1)
где Gm — тензор Эйнштейна, { — гравитационная постоянная Эйнштейна, Тт — тензор энергии-импульса материи, определямый выражением
2 6Sm
Соответствующим выбором координат для данного решения можно получить диагональную метрику, задающую квадрат линейного элемента в виде
ds2 = f 1 — R^ dt2 ~—ц ~ r2(dd2 + sin2 в ■ d'2). (3)
rZ 1 - R
Здесь и во всех дальнейших выкладках предполагается, что сигнатура метрики (+, —, —, —), скорость света c = 1, а R — радиус Шварцшильда.
Можно заметить, что в таких координатах метрика статична, по крайней мере, за пре­делами радиуса Шварцшильда для любого, в том числе для движущегося, сферически симметричного распределения материи. В эти же условия погружается и задача о коллапсе сферического ограниченного тела, которая будет рассматриваться в дальнейшем. По тео­реме Биркгофа решение в виде геометрии Шварцшильда единственно для пустой области пространства со сферической симметрией [2], т.о. можно утверждать, что именно геометрия Шварцшильда описывает ту область пространства, которая является внешней по отноше­нию к коллапсирующей материи.
1.2 Вечные черные дыры и мотивировка задачи о коллапсе
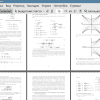
В случае, когда гравитирующая материя полностью сосредоточена под собственным гра­витационным радиусом, геометрия Шварцшильда описывает пространство в том числе и под гравитационным радиусом. Описание движения с помощью геометрии Шварцшильда в таких условиях приводит к предсказанию достаточно интересной структуры геодезических и, вообще, любых мировых линий частиц. Тот факт, что любая материя, и в том числе свет, попав под гравитационный радиус, уже не могут выйти наружу, приводит к тому, что данное массивное тело называется черной дырой. В случае, когда вся материя располо­жена в центральной сингулярности, черная дыра называется вечной. Для вечной черной дыры можно изучить всю структуру риманова многообразия путем перехода от описания геометрии в Шварцшильдовских координатах, имеющего координатную особенность при r = R, к описанию той же самой геометрии в каких-либо других координатах, в которых эта особенность отсутствует. Одним из примеров координатной системы, покрывающей всю структуру риманова многообразия, является координаты Крускала-Шекереса [2].
Рис. 1: Диаграмма Крускала - Шекереса
На приведенной на Рис.1 диаграмме описана структура многообразия в случае вечной черной дыры. Как видно, на ней кроме нашей вселенной и черной дыры присутствуют еще одна сингулярность (так называемая белая дыра) и еще одна область, симметричная нашей вселенной, которую можно трактовать, как некоторую параллельную вселенную. На опыте, однако, никакие явления, показывающие наличие белой дыры не наблюдаются. Если же рассматривать коллапс некоторой реальной звезды, то осмысленной остается толь­ко часть диаграммы, отсеченная кривой rm(t), соответствующей мировой линии частицы, расположенной на поверхности коллапсирующей звезды, потому что геометрия Шварц­шильда имеет место только в области, в которой отсутствует материя. Для описания же пространства внутри коллапсирующей звезды нужно решать уравнения Эйншейна в при­сутствии материи одновременно с уравнениями движения самой материи, что в общем слу­чае представляет довольно сложную задачу. Однако, в некоторых частных случаях такие решения были найдены. Анализ пространства внутри коллапсирующей звезды необходим для описания полной структуры многообразия, поэтому решение некоторых частных задач представляет большой интерес. В данной работе исследуется коллапс шара, состоящего из пылевидной материи. Выбор пылевидной материи упрощает задачу тем, что все частицы материи движутся, не отклоняясь от геодезических, и уравнения движения пылевидной ма­терии следуют из уравнений гравитационного поля. Оставшиеся уравнения поля допускают дальнейший анализ, позволяющий описать геометрию внутри сферы.
1.3 Подход к гравитации в форме теории вложения
Теория вложения — подход к гравитации, в котором искривленное пространство-время рас­сматривается как риманово многообразие, вложенное в плоское пространство большего числа измерений. Он был впервые предложен Редже и Тейтельбоймом в работе [3]. Со­гласно теореме Жане-Картана, обобщенной А.Фридманом [4] на псевдоевклидов случай, такое вложение в общем случае локально существует, если объемлющее пространство имеет N > d(d+1) измерений, по крайней мере одно из которых времениподобное, а три — про­странственноподобные. Предполагается также аналитичность метрики, в противном слу­чае, ограничение должно быть усилено. Следовательно для 4-х мерного пространства долж­но хватать 10 измерений. В случае же наличия дополнительных симметрий у пространства времени, размерность объемлющего пространства может быть значительно снижена.
В таком подходе многообразие задается как поверхность, набором функций вложения y“(x^), зависящих от координат на многообразии, и преобразующихся как скаляр отно­сительно общековариантной группы преобразваний координат на многообразии. Метрика, определяющая многообразие, считается индуцированной, то есть отвечающей измерению малых расстояний по метрике объемлющего пространства. Она определяется функциями вложения согласно следующей формуле
9^v = gabd^yadv yb, (4)
где yab — метрика объемлющего пространства. При построении вложения заданной геомет­рии, равенство (4) можно воспринимать как уравнения на функции вложения.
Изучение геометрии вложенной поверхности оказывается полезным для анализа пол­ной структуры многообразия. Например, упоминавшиеся ранее диаграммы Крускала тесно связаны с вложением Фронсдала [5] для вечной черной дыры. В связи с этим возникает интерес к описанию в терминах теории вложения черной дыры с распределенной матери­ей или коллапса, в результате которого происходит образование горизонта черной дыры. Эта задача обладает меньшей симметрией, чем задача вложения вечной черной дыры, для которой существует набор известных решений, представленный в книге [6].
Купить