ФРАГМЕНТАЦИЯ ЦВЕТНОЙ СТРУНЫ И БЛИЖНИЕ БЫСТРОТНЫЕ КОРРЕЛЯЦИИ ВО ВЗАИМОДЕЙСТВИЯХ АДРОНОВ ВЫСОКИХ ЭНЕРГИЙ

1 Введение 3
1.1 Корреляции (Д' Ду) 3
1.2 Обозначения 3
1.3 Цель работы 4
2 Вычисления 4
2.1 Постановка задачи 4
2.2 Преобразования Лоренца 4
2.3 Выражения для Д' ж Ду 5
2.4 Распределение p(kx, kz) 6
2.5 Замены переменных 6
2.6 Области определения и неодназначность переменных 7
2.7 Вычисление р(Д', Ду) 7
2.8 Графики 11
3 Связь с другими моделями 11
3.1 Поведение балансной функции В(Ду, Д') 11
3.2 Объединение с моделью одиночной струны 14
4 Заключение 15
Список литературы 16
Купить

В адронных столкновениях типа протон-протон при сверх высоких энергиях образу­ется множество частиц основная часть из которых - л-мезоны. Считается, что процесс происходит через промежуточное состояние - кварк-глюонную плазму. После остывания плазмы из нее образуются частицы, многие из которых распадаются не успевая долететь до детекторов. Известно, что порядка 70% задетектированных заряженных л-мезонов по­лучаются от распада первичных р-мезонов по сильному взаимодействию. Данная работа описывает влияние подобных распадов на распределение л-мезонов по направлениям раз­лета, в частности на распределение двухчастичных корреляций (Д' Ду).
1.1 Корреляции (Д' Ду)
Для описания столкновений при сверхвысоких энергиях удобно использовать специ­альные переменные. Везде в данной работе будем считать, что ось столкновения протонов сонаправленна с осью z Пусть р, E импульс и энергия образовавшейся частицы. Импульс вдоль оси z принято описывать переменной
E + pz
E - pz
которая называется быстротой в направлении z. Для краткости мы будем называть ее просто быстротой. В плоскости перпендикулярной к оси z импульс описывается обычными полярными координатами (p?, '), где p? = y/pX + / Д, а ' есть угол между проекцией р на эту плоскость и осью х. Угол ' изменяется в пределах от —л до л. Таким образом импульс при известной энергии однозначно описывается тремя переменными (у, ',p?). Нас будут интересовать переменные (у,'), т. к. они связанны с направлением.
Сами по себе распределения по (у,') мало содержательны. Из азимутальной симмет­рии эксперимента следует, что распределение образовавшихся частиц по ' равномерное. Так же из эксперимента известно, что распределение образовавшихся частиц по у прибли­зительно равномерно в некотором интервале [ут™, утах] и равно нулю вне этого интервала. Эти распределения называются одночастичными.
Гораздо сложнее и содержательнее выглядят двухчастичные распределения или двух­частичные корреляции. В них рассматриваются всевозможные пары образовавшихся ча­стиц и их координаты (', '2, у1, у2). Из сказаного выше ясно что нетривиально могут быть распределены лишь комбинации Д' = '1 — '2, Ду = у1 — у2- Ниже будут рассматриваться двумерное распределение (Д', Ду) и влияние на него распадов р-резонансов.
1.2 Обозначения
Будем обозначать за px(a) - плотность распределения величины x в точке x = а. Если из названия точки сразу ясно по какой величине растределение, индекс будем опускать: p(x) = px (x). Плотность распределения нормирована
+1
/dx ри=i,
поэтому вычисления достаточно проводить с точностью до множителя, который всегда можно восстановить из условий нормировки.
1.3 Цель работы
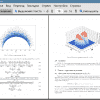
Цель работы - найти р(Д', Ду) для двух %-мезонов, которые образовались из распа­да р-мезона летяшего с некоторым импульсом. Как мы увидим в дальнейшем, подобная модель приводит к образованию "вулканообразного" пика в точке Д' = 0, Ду = 0. Дан­ный пик действительно наблюдается в различных экспериментальных данных (например в [1]).
Купить