Введение 2
Глава 1. Обзор литературы 14
1.1. Методы оценки матриц корреспонденций 15
1.2. Оценка матрицы корреспонденций при помощи ин­формации с датчиков 20
Глава 2. Математическая модель оценки матрицы корреспонден­ций на сети из параллельных маршрутов 31
2.1. Распределение транспортных потоков в прямой и двой­ственной постановке 33
2.2. Оценка матрицы корреспонденций как задача обрат­ная к равновесному распределению потоков 37
Глава 3. Математическая модель оценки матрицы корреспонденций на сети произвольной топологии 41
3.1. Распределение транспортных потоков в прямой и двой­ственной формулировке 41
3.2. Двухуровневая задача оценки матрицы корреспонденций на основе информации с датчиков фиксации но­мерных знаков 44
Глава 4. Эксперимент на транспортной сети Санк-Петербурга 47
Заключение 51
Список литературы 53
Купить

В современном мире мы все чаще сталкиваемся с проблемами на доро­гах: автомобильные пробки, снижение скорости сообщения, растущее число дорожно-транспортных происшествий, резкое увеличение количества авто­мобилей, которое в свою очередь приводит к нехватке мест для парковки и загрязнению окружающей среды (рис.1). Решение этих проблем требует ре­организации дорожного движения и модернизации улично-дорожной сети (УДС) города. В мировой практике активно применяется, например, огра­ничение въезда в центр города, взымание платы за стоянку в определен­ной городской зоне, строительство перехватывающих парковок и платных участков дорог, ограничение владения личным транспортом, использование интеллектуальных транспортных систем (ИТС) и т.д. Однако результатив­ность таких подходов не везде одинакова [6].
Рис. 1. Проблемы на транспортной сети
Одной из наиболее острых проблем, препятствующих устойчивому раз­витию транспортной системы нашей страны, является резкое повышение уровня загрузки автомобильных дорог транспортными потоками, в первую очередь, на территории крупных городов и на подходах к ним. Следствием этого являются перечисленные ранее проблемы.
По данным Федерального дорожного агентства около 30% автомобиль­ных дорог федерального значения работают в режиме перегрузки (в первую очередь — на подходах к крупным городам). Наиболее остро проблема пере­груженности проявляется в крупнейших и сверхкрупных городах, в которых уровень автомобилизации давно перешагнул уровень 300 автотранспортных средств (АТС) на 1000 жителей. Средние скорости сообщения в городах неуклонно снижаются, и нередко достигают 8-10 км/час, при оптимальных 30-35 км/час. Согласно имеющимся оценкам, суммарные дополнительные издержки, связанные с перегрузкой дорожной сети, достигают в России 4­9% ВВП в год [11].
Исследования проблемной области в отечественной и зарубежной ли­тературе говорят о том, что развитие современных методов организации дорожного движения (ОДД), основанных на применении интеллектуальных транспортных технологий и математических моделей, напрямую влияет на возможности повышения пропускной способности дорожных сетей и уров­ня безопасно сти дорожного движения. При системной реализации матема­тического подхода к ОДД и совершенствованию транспортной сети мож­но резко повысить эффективность управления дорожным движением, зна­чительно улучшить ситуацию на дорогах, улучшить устойчивость работы транспортной системы в целом и качество жизни населения в городах.
Опыт передовых зарубежных стран свидетельствует, что эффект от внед­рения в городах современных сетевых проектных решений по ОДД, разра­батываемых с использованием математических моделей транспортных по­токов, выражается в сокращении числа ДТП на величину около 15%, уве­личении пропускной способности дорожных сетей до 20%, снижении по­треблении топлива на величину до 20%. Косвенные экономические эффек­ты, связанные с предотвращением транспортных заторов и обеспечением устойчивой работы автомобильного транспорта, включают прирост ВВП (до 10%) и повышение занятости населения [11].
Как сказано ранее, оптимальное планирование транспортных сетей в смысле улучшения организации дорожного движения требует применения аппарата математического моделирования, на основе которого возможно определение и прогноз всех параметров функционирования УДС. В самом общем смысле можно выделить три класса математических моделей, при­менимых для анализа транспортных сетей [14]:
• прогнозные модели;
• имитационные модели;
• оптимизационные модели.
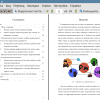
Построение математической модели требует формализации транспорт­ной сети. Дорожная сеть представляется в виде графа, узлы которого со­ответствуют перекресткам, а дуги — участкам улиц. Изучаемый город или район делится на некоторое условное число районов отправления и прибы­тия (фиксированное множество узлов графа). Общий объем перемещений между районами отправления и прибытия ^П-парами) в определенный пе­риод времени называется межрайонной корреспонденцией в этот период. Получив все значения межрайонных корреспонденций, можно со ставить матрицу корреспонденций. На рисунке 2 представлен пример формализа­ции транспортной сети в виде графа, а на рисунке 3 — пример составления матрицы корреспонденций в виде таблицы, где на пересечении i-й стро­ки и j-го столбца стоит объем транспортных средств, передвигающихся из района i в район j в определенный период времени.
Прогнозные модели предполагают, что известны топология, характери­стики транспортной сети и расположение потокообразующих объектов в городе и необходимо определить, какими будут транспортные потоки меж­ду этими объектами [14].
Рис. 2. Пример формализации транспортной сети в виде графа
Такие модели позволяют прогнозировать последствия изменений в транспортной сети или в размещении объектов. В свою очередь имитационное моделирование воспроизводит все детали движения, в том числе развитие процесса во времени. При этом усредненные значения потоков и распределения по путям заранее известны. Отличие этих двух моделей можно кратко сформулировать следующим образом. Прогнозные модели отвечают на вопрос: «только и куда» будут ехать в данной сети. Имитационные модели отвечают на вопрос: как в деталях будет происхо­дить движение, если известно в среднем, «сколько и куда» [14]. Прогнозные и имитационные модели ставят своей целью адекватное воспроизведение транспортных потоков, в то время как оптимизационные модели отвечают на вопросы оптимизации функционирования транспортных сетей. Рассмот­рим эти три класса моделей более подробно.
Рис. 3. Представление матрицы корреспонденций в виде таблицы
Прогнозные модели
Общую схему прогнозных моделей можно свести к следующим трем взаимосвязанным задачам [13]:
• расчет общих объемов передвижения между районами города или агло­мерации (расчет матриц межрайонных корреспонденций);
• распределение корреспонденций по конкретным путям в транспортной сети;
• расчет загрузки всех элементов сети транспортными потоками.
К числу наиболее распространенных моделей расчета корреспонденций относятся гравитационные, энтропийные, модели конкурирующих и проме­жуточных возможностей Стауффера [14].
Загрузка транспортной сети определяется количеством транспортных средств, которые используют для своего передвижения элементы сети. Загрузка эле­ментов моделируется посредством распределения межрайонных корреспон­денций по конкретным путям, соединяющим пары районов. Входные дан­ные для такой модели — матрица корреспонденций, а ее цель — определение для каждой пары районов отправления-прибытия набора путей, используе­мых для перемещения между этими районами.
Существует классификация моделей загрузки транспортной сети, осно­ванная на следующих признаках [14]:
• модели, основанные на нормативном (нацеленном на поиск системного оптимума) и дескриптивном (определяющем результат пользовательской оптимизации маршрутов) подходе;
• статические и динамические модели.
Для определения объемов загрузки УДС необходимо выявить правила, по которым водители выбирают тот или иной маршрут следования. Пове­денческие принципы пользователей были окончательно сформулированы в работе [48] в виде двух принципов:
• пользователи сети независимо друг от друга выбирают маршруты сле­дования, соответствующие их минимальным транспортным расходам,
• пользователи сети выбирают маршруты следования, исходя из миними­зации общих транспортных расходов в сети,
которые получили названия соответственно первого и второго принципа Вардропа [2].
Распределение транспортных потоков согласно первому принципу Вар- дропа соответствует конкурентному бескоалиционному равновесию, пред­полагающему совершенный эгоизм участников дорожного движения — каж­дый стремится достигнуть конечного пункта своей поездки как можно быст­рее и из имеющихся возможных вариантов следования выбирает тот марш­рут, по которому будет нести минимальные затраты (временные, финансо­вые, моральные и т.п.) на проезд. Этот принцип в полной мере учитыва­ет фактор взаимного влияния пользователей. Поэтому его также называют конкурентным равновесием (user equilibrium). Суть этого принципа крат­ко можно сформулировать так: при равновесном распределении загрузки ни один из участников движения не может изменить свой путь так, чтобы уменьшить свое индивидуальное время поездки. Второй принцип Вардро- па предполагает централизованное управление движением в сети. Соответ­ствующее ему распределение транспортных потоков называют системным оптимумом (system optimum). Примером пользователей, передвигающихся согласно второму принципу, служат водители маршрутизированного транс­порта.
Имитационные модели
К классу имитационных по их функциональной роли можно отнести ши­рокий спектр моделей, известных под названием модели динамики транс­портного потока. В моделях этого класса может применятся разная техни­ка — от имитации движения каждого отдельного автомобиля до описания динамики функции плотности автомобилей на дороге. При этом для дина­мических моделей характерна значительно большая детализация движения и, соответственно, потребность в больших вычислительных ресурсах. При­менение этих моделей позволяет оценить динамику скорости движения, за­держки на перекрёстках, длины и динамику образования «очередей» или «заторов» и другие характеристики движения. Основные области практиче­ского применения динамических имитационных моделей — улучшение ор­ганизации движения, оптимизация светофорных циклов и др. В настоящее время актуальной задачей является разработка систем автоматизированно­го оперативного управления движением, работающих в режиме реального времени. Однако помимо практического применения, развитие динамиче­ских моделей представляет большой научный интерес в связи с изучением транспортного потока как физического явления со сложными и нетривиаль­ными свойствами. Среди таких свойств — спонтанная потеря устойчивости, явления самоорганизации и коллективного поведения и многие другие.
Большинство существующих моделей динамики транспортных потоков может быть приблизительно разделено на три класса:
• макроскопические модели;
• микроскопические модели;
• стохастические модели.
В макроскопических моделях движение транспортных средств уподобля­ется какому-либо физическому потоку (гидро- и газодинамические модели). В микроскопических моделях существенно предположение о наличии связи между перемещением ведомого и головного автомобиля. По мере развития теории в моделях этой группы учитывалось время реакции водителей, ис­следовалось движение на многополосных дорогах, изучалась устойчивость движения. Этот класс моделей также называют моделями следования за лидером. В стохастических моделях транспортный поток рассматривается как результат взаимодействия транспортных средств на элементах транс­портной сети. В связи с жестким характером ограничений сети и массовым характером движения в транспортном потоке складываются отчетливые за­кономерности формирования очередей, интервалов, загрузок по полосам дороги и т. п. Эти закономерности носят существенно вероятностный ха­рактер.
Модели динамики транспортных потоков дают достаточно простые устой­чивые решения в случае малой загрузки дорог (свободное движение при из­быточном ресурсе). Однако решения для случая высокой плотности потоков чрезвычайно чувствительны к малейшим флуктуациям параметров дорог и особенностей поведения участников движения.
Оптимизационные модели
В классе оптимизационных моделей решаются задачи оптимизации марш­рутов пассажирских и грузовых перевозок, выработки оптимальной конфи­гурации сети и другие. В частности, рассматриваются задачи оптимизации работы дорожной системы на участке протяжённостью несколько километ­ров с движением автомобилей в одном направлении. При разработке планов оптимизации указанной системы используются модели двух типов [3]. Пер­вой из них является модель для оценки транспортной загрузки у узкого места, а второй — модель линейного программирования. В обоих случаях в качестве контрольного параметра используется полная пропускная спо­собность дороги и делается попытка в каждом узком месте поддерживать транспортную нагрузку меньше пропускной способности. Транспортная на­грузка у узкого места дороги образуется за счёт автомобилей, въезжающих на магистраль с примыкающих въездов, расположенных перед узким ме­стом. Если известна интенсивность каждого такого потока, то можно оце­нить транспортную нагрузку у данного узкого места.
Для анализа и планирования работы дорожной системы в установив­шемся режиме могут использоваться различные модели линейного програм­мирования. В простейшем случае модель имеет следующий вид:
п
Е *>
;=1
при условиях
п
AjkXj 6 Вк, к = 1,..., п,
j=1
х 6 D, j = 1,...,п,
Xj > 0, j = 1,...,п.
В данной модели Xj — интенсивность j -го входящего потока; Dj — транспортная нагрузка на j -м въезде; Вк — пропускная способность к -го узкого места, а Ajk — вероятность того, что автомобиль, попадающий на магистраль с j -го въезда, пройдёт через к -ое узкое место. Построенная модель максимизирует выходящий поток системы. Первая система ограни­чений требует, чтобы в каждом узком месте дороги транспортная нагрузка не превышала полной пропускной способности в данном направлении. Вто­рая система ограничений требует, чтобы интенсивность входящего потока не превышала транспортной нагрузки при любом входящем потоке. Третья система ограничений гарантирует возможность решения.
В этой модели могут быть использованы и другие ограничения: ограни­чения, устанавливающие максимальную длину очереди на всех регулируе­мых въездах; ограничения, гарантирующие, что транспортная нагрузка не превысит пропускной способности узкого ме ста дороги на наиболее ответ­ственной полосе движения.
Задача поиска матриц корреспонденций явно входит только в прогноз­ные модели. Однако, без решения этой задачи невозможно представить се­бе эффективной реализации и адекватного применения имитационных и оптимизационных моделей на реальных транспортных сетях. В самом де­ле, практическое применение результатов математического моделирования в конечном счете сводится к мероприятиям по реорганизации дорожного движения или изменению инфраструктуры транспортной сети, эффективная реализация которых невозможна без достоверной информации о трафике, точность и своевременность которой зависят от технических возможностей расчета матриц корреспонденций между выделенными на транспортной се­ти районами отправления-прибытия [2].
В связи с этим важно отметить, что получать данные о межрайонных корреспонденциях можно не только при помощи описанных выше матема­тических моделей, но и другими способами: натурными замерами, прове­дением социологических опросов, при помощь счетчиков. Однако, стоит отметить, что такие способы крайне трудозатратны и малоэффективны. На сегодняшний день существуют и другие способы получения информации для матрицы корреспонденций, например, при помощи различных датчиков, установленных на транспортной сети, и RFID-меток. RFID-метка, напри­мер, передает радиосигнал с транспортного средства на пульт управления, что позволяет проследить весь путь его следования и однозначным образом построить матрицу корреспонденций. К сожалению, на сегодняшний день RFID-система не получила широкого распространения, но является крайне перспективной с точки зрения полноты получаемых данных.
В то же время датчики регистрации транспортных средств уже сего­дня активно используются на дорогах. Эти датчики обладают различными функциями, какие-то из них многофункциональны. Некоторые из них фик­сируют потоки, собирают статистическую информацию об интенсивности движения, количестве автомобилей (петлевые детекторы [41]), некоторые могут фиксировать номерные знаки (датчики фиксации номерных знаков) или скорость движущихся транспортных средств.
Датчики регистрации номерных знаков в своем большинстве установле­ны для фиксации нарушений правил дорожного движения, но могут быть активно использованы для получения информации о межрайонных корре­спонденциях или о времени движения по участку дороги. Распознавая но­мерной знак транспортного средства на разных элементах сети в последо­вательные моменты времени, мы получем однозначную картину маршрута, по которому это транспортное средство двигалось, или времени, за кото­рое транспортное средство преодолевает конкретный участок. Кроме того, проанализировав маршруты движения всех транспортных средств, можно получить межрайонные корреспонденции и саму матрицу корреспонден­ций. Однако не всегда есть возможность сделать наблюдаемыми все дуги транспортной сети. Количество датчиков может быть ограничено бюдже­том, выделяемым на их закупку и установку. Тогда появляется задача вос­становления потоков на ненаблюдаемых дугах, а соответственно и задачи оценки и восстановления матрицы корреспонденций. Получив время дви­жения потоков по дугам транспортной сети, возникает вопрос: можно ли по этим данным оценить корреспонденции? В следующих главах будет проде­монстрировано, что решить задачу оценки матрицы корреспонденций мож­но и при помощи информации о времени движения транспортных средств по участкам УДС.
Данная работа организована следующим образом. В Главе 1 рассматри­вается обзор литературы по теме оценки матрицы корреспонденций. Гла­ва 2 описывает разработанный подход к оценке матрицы корреспонденций, как к решению двойственной задачи распределения транспортных потоков по первому принципу Вардропа на сети, состоящей из одной пары райо­нов отправления-прибытия и параллельных маршрутов между ними. Двой­ственная по становка задачи к равновесному распределению потоков на сети произвольной топологии рассматривается в Главе 3, как и двухуровневая за­дача оценки матрицы корреспонденций на основе информации с датчиков фиксации номерных знаков. В Главе 4 описан эксперимент, проведенный на транспортной сети Санкт-Петербурга. В Заключении даются выводы об эффективности разработанной модели.
Купить