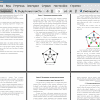
Тема: Раскраска графов и задача построения расписания с ограничениями

Теория графов активно развивается на протяжении последних нескольких десятилетий. Связано это с тем, что стремительно расширяется область приложений теории графов, увеличивается количество задач, которые могут быть решены посредством методов теории графов. Так, например, основополагающей для задач, связанных с навигацией и построением сетей, является задача нахождения кратчайшего пути на графе. Другой актуальной задачей является задача составления расписаний. Задача подразумевает составление абсолютно любого расписания: от школьного расписания до порядка проведения работ на предприятии. Ограничениями в данной задаче является невозможность проведения заданий (уроков, работ и т. п.) одновременно по ряду причин. Подобная задача возникает постоянно в различных ситуациях, поэтому для её решения необходим эффективный алгоритм.
Одной из трудных задач теории графов является задача отыскания хроматического числа графа, то есть минимального числа цветов, необходимых для раскраски вершин графа. Предложены различные алгоритмы решения данной задачи, однако поиск эффективного алгоритма продолжается. Раскраска вершин позволяет моделировать многие проблемы планирования. В частности, при помощи алгоритма раскраски графа может быть решена задача составления расписания.
В рамках данной работы рассматривается сведение задачи составления расписания с ограничениями к задаче о вершинной раскраске графа, осуществляется анализ алгоритма вершинной раскраски графа, предложенный Красновой А. Ю. [1] и предлагается альтернативный алгоритм раскраски графа.
План работы:
1. Задача раскраски графа и рассмотрение существующих алгоритмов её решения.
2. Реализация и анализ алгоритма, предложенного Красновой А. Ю. [1].
3. Разработка алгоритма решения задачи раскраски графа.
4. Сравнение результатов работы алгоритмов, реализованных в пунктах 2 и 3.
5. Сведение задачи составления расписания с ограничениями к задаче раскраски графа и применение разработанного алгоритма к её решению.
В первой главе работы приведены некоторые определения из теории графов, используемые в работе (граф, смежные вершины, матрица смежности), описывается задача раскраски графа, её варианты, а также подходы к нахождению неточного решения: последовательный перебор, жадные алгоритмы и алгоритмы с использованием битовых операций.
Вторая глава описывает схему и реализацию алгоритма, предложенного Красновой А. Ю., и разработанного в рамках данной работы алгоритма. В заключении главы представлено сравнение работы на коллекции DIMACS- файлов.
Третья глава посвящена задаче о составлении расписания. В начале главы приводится постановка задачи в её самом простом случае и вариант усложнения задачи. Далее в главе рассмотрен пошагово способ решения задачи: от исходных данных до результата. В конце главы приводится пример задания на тестовом расписании.
В заключении перечислены результаты работы и приводятся примеры разработок программных продуктов для составления расписания.
Купить

Составление расписаний является неотъемлемой частью повседневной жизни. Зачастую при составлении расписания изначально известно только то, что необходимо сделать и что нельзя сделать одновременно. Оптимально составленное расписание способно принести большую выгоду, но при этом поиск такого расписания может занять длительное время. Для ускорения процесса необходим способ решать данную задачу с использованием современных технологий.
Одним из способов нахождения расписания является сведение этой задачи к важной задаче теории графов - задаче о раскраске графа. Поиск методов эффективного решения последней продолжается и сейчас.
В данной работе проведен анализ алгоритма вершинной раскраски графа, предложенный Красновой А. Ю., предложен новый алгоритм вершинной раскраски графа и проведено сравнение работы рассмотренных алгоритмов раскраски на коллекции графов. Полученный алгоритм раскраски вершин графа был применен к решению задачи составления расписаний и осуществлена программная реализация для демонстрации работоспособности предложенного подхода.
Купить