
Тип работы:	Предмет:	Язык работы:

Моделирование изгиба защемленной пластинки методом начальных функций

Работа №	125705
Тип работы	Магистерская диссертация
Предмет	математическое моделирование
Объем работы	71
Год сдачи	2017
Стоимость	5550 руб.
ПУБЛИКУЕТСЯ ВПЕРВЫЕ
Просмотрено	69

Не подходит работа?

Узнай цену на написание

Содержание

Введение 3
Постановка задачи 4
Обзор литературы 6
Глава 1. Метод начальных функций в задаче изгиба пластинки 8
1.1 Метод начальных функций 9
1.2 Частное решение 11
1.3 Общее решение однородного уравнения 12
Глава 2. Моделирование изгиба жестко защемленной пластинки 16
2.1 Удовлетворение граничным условиям 16
2.2 Поиск разрешающей функции ф (n) 18
2.3 Поиск частного решения неоднородной системы 19
2.4 Напряженно-деформированное состояние пластинки 19
2.5 Удовлетворение оставшимся граничным условиям 23
Глава 3. Вычислительный эксперимент 26
3.1 Процесс моделирования изгиба пластинки 26
3.2 Основные параметры модели 27
3.3 Оценка адекватности построенной модели 28
3.4 Оценка точности построенного решения 33
3.5 Сравнение построенных алгоритмов приближения 35
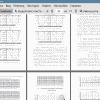
3.6 Результаты моделирования изгиба пластинки 39
Выводы 52
Заключение 54
Список литературы 55
Приложение A 59
Приложение B 63
Приложение C 64
Приложение D 66
Приложение E 68
Приложение F 71

Введение

Задачи прикладной теории упругости, в частности, о нагруженных пластинках с различными условиями закрепления и условиями нагрузки: жесткое защемление всех сторон, защемление только двух сторон, консольные пластинки (с защемлением только одной стороны), шарнирно- опертые пластинки, с равномерной нагрузкой, с сосредоточенной силой и др., не теряют актуальности по сей день [1-7]. Результаты исследований и расчетов активно применяются в строительной, судо-, авиа- и ракетостроительной отраслях, машиностроении и др.
В данной работе рассматривается одна из задач прикладной теории упругости: моделирование изгиба равномерно нагруженной тонкой жестко защемленной прямоугольной изотропной пластинки. Задача об изгибе такой пластинки представляет из себя двумерную краевую задачу, не имеющую точного аналитического решения, в связи с чем большую популярность приобретают не только численные решения, но и приближенные аналитические.
Процесс моделирования изгиба в данном исследовании основан на известном методе начальных функций, предложенным А. И. Лурье [8, 9] и В. З. Власовым [10], с использованием операторного исчисления, представленного В. А. Агаревым в [11]. Метод начальных функций позволяет построить аналитическое решение задачи, сводящееся к решению системы линейных алгебраических уравнений бесконечной размерности. Поэтому в данной работе также будут предложены и подробно рассмотрены три алгоритма (в том числе будут приведены результаты проведенного моделирования), позволяющих построить приближенно-аналитическое решение поставленной задачи путем ограничения размерности такой системы.

Возникли сложности?

Нужна помощь преподавателя?

Помощь студентам в написании работ!

ДИПЛОМНЫЕ МАГИСТЕРСКИЕ ДИССЕРТАЦИИ

Курсовые Статьи Диплом Рязань

Заключение

В данной работе была рассмотрена одна из задач прикладной теории упругости — задача о равномерно нагруженной тонкой прямоугольной пластинке, края которой жестко зафиксированы. Для ее решения была построена математическая модель такой пластинки с использованием метода начальных функций. Решение данной задачи было получено в приближенно-аналитическом виде, которое на двух противоположных краях пластики даст точные результаты, а на двух оставшихся — приближенные. Точность приближения в данной модели регулируется двумя параметрами: размерность системы линейных алгебраических уравнений, которую надо решить, чтобы получить все компоненты, описывающие напряженно-деформированное состояние такой пластинки, и точность компьютерного вычисления.
Для приближения было предложено два немодифицируемых метода, качество которых напрямую зависит от размерности системы, и один модифицируемый метод, включающий достоинства двух предыдущих метода, качество которого будет зависеть не только от размерности системы, но и от модификации самого алгоритма.
Построенная модель может быть в дальнейшем модифицирована для решения других схожих задач, связанных с пластинкой, например для другого вида нагрузки, или для другого закрепления самой пластинки. Также можно модифицировать последний предложенный алгоритм приближения таким образом, чтобы требуемая точность решения достигалась при меньших размерностях СЛАУ, и вычислить оптимальное количество точек для заданного N, что позволит уменьшить временные и другие вычислительные затраты.
Результаты данного исследования могут быть использованы в различных, более сложных, задачах, использующих жестко защемленные пластинки.

Литература

[1] Ушаков А. Ю., Ванюшенков М. Г. Расчет сжато-изогнутых пластинок со смешанными вдоль края граничными условиями методом начальных функций // Промышленное и гражданское строительство, 2016. № 11. С. 14-18.
[2] Ванюшенков М. Г., Ушаков А. Ю. Определение критической сжимающей нагрузки упругих тонких пластинок методом начальных функций // Промышленное и гражданское строительство, 2010. № 11. С. 71-73.
[3] Волошановская Ю. Э. Расчет тонкой квадратной жестко защемленной на двух противоположных краях плиты методом начальных функций // Наука, Техника, Инновации 2014: сборник статей Международной научно-технической конференции / Под общей редакцией А. Л. Сафонова. Брянск: НДМ, 2014. С. 367-370.
[4] Kennedy J. B. Clamped Skew Plate under Uniform Normal Loading // The Aeronautical Journal, 1968. Vol. 72, No 688. P. 338-339.
[5] Young D. Clamped Rectangular Plates with a Central Concentrated Load // The Aeronautical Journal, 1940. Vol. 44, No 352. P. 350-354.
[6] Imrak C. E., Gerdemeli I. A numerical method for clamped thin rectangular plates carrying a uniformly distributed load // International Applied Mechanics, 2007. Vol 43, No 6. P. 701-705.
[7] Лычев С. А., Салеев С. В. Замкнутое решение задач об изгибе жестко закрепленной прямоугольной пластины // Вестник Самарского университета. Естественнонаучная серия, 2006. № 2. С. 62-73.
[8] Лурье А. И. К теории толстых плит // Прикладная математика и механика, 1942. Т. 6. Вып. 2-3. С. 151-168.
[9] Лурье А. И. Пространственные задачи теории упругости. М.: ГИТТЛ, 1955. 491 с.
[10] Власов В. З., Леонтьев Н. Н. Балки, плиты и оболочки на упругом основании. М.: Физматгиз, 1960. 491 с.
[11] Агарёв В. А. Метод начальных функций для двумерных краевых задач теории упругости. Киев: Изд. АН УССР, 1963. 204 с.
[12] Коялович Б. М., Об одном уравнении с частными производными четвертого порядка. СПб.: тип. Имп. Акад. наук, 1902. 125 с.
[13] Коялович Б. М. Исследования о бесконечных системах линейных уравнений // Изв. Физ.-матем. ин-та им. В. А. Стеклова, 1930. Т. 3. С. 41-167.
[14] Бубнов И. Г. Строительная механика корабля: Ч. 1-2 СПб.: тип. Мор. м-ва, 1912-1914. 2 т.
[15] Галеркин Б. Г. Упругие тонкие плиты. Госстройиздат, 1933. 371 с.
...