Тема: О взаимосвязи решений второй задачи Золотарева и полиномиальной задачи
Закажите новую по вашим требованиям
Представленный материал является образцом учебного исследования, примером структуры и содержания учебного исследования по заявленной теме. Размещён исключительно в информационных и ознакомительных целях.
Workspay.ru оказывает информационные услуги по сбору, обработке и структурированию материалов в соответствии с требованиями заказчика.
Размещение материала не означает публикацию произведения впервые и не предполагает передачу исключительных авторских прав третьим лицам.
Материал не предназначен для дословной сдачи в образовательные организации и требует самостоятельной переработки с соблюдением законодательства Российской Федерации об авторском праве и принципов академической добросовестности.
Авторские права на исходные материалы принадлежат их законным правообладателям. В случае возникновения вопросов, связанных с размещённым материалом, просим направить обращение через форму обратной связи.
📋 Содержание
1 Вспомогательные сведения 3
1.1 Полиномиальная задача 3
1.1.1 Постановка полиномиальной задачи 3
1.1.2 Полиномы Чебышёва 4
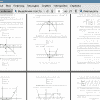
1.1.3 Решение полиномиальной задачи при n = 2 6
1.1.4 Решение полиномиальной задачи при n = 3 8
1.2 Постановка второй задачи Золотарева 11
1.3 Связь полиномиальной задачи с задачей Золотарева 11
1.4 Постановка задачи 12
2 Обзор литературы 13
3 Основные результаты 14
3.1 Алгоритм решения второй задачи Золотарева 14
3.2 Решение задачи Золотарева при n = 2 14
3.3 Решении задачи Золотарева при n = 3 18
4 Основные выводы работы 19
ЛИТЕРАТУРА 20
📖 Введение
При этом наиболее привлекательными являются задачи, обладающие альтернансными условиями, поскольку имеют самое широкое применение в теории электрических цепей, в частности при синтезе фильтров.
Рассматриваемые в настоящей работе задачи Золотарева и полиномиальная относятся именно к такому классу задач.
В предлагаемой работе проводится подробный анализ решений второй задачи Золотарева и полиномиальной при n = 1, 2 и n = 3 как в отдельности, так и их взаимосвязи. Целью работы было изучить возможность получения решения задачи Золотарева через решение полиномиальной задачи.
✅ Заключение
1. При n = 2 получены явные формулы зависимости А(Л). Решение задачи Золотарева через полиномиальную можно записать в аналитическом виде.
2. При n = 3 можно определить значение А(Л) для конкретных заданных параметров при отсутствии явных формул А(Л). Поэтому решение задачи Золотарева можно получить через полиномиальную, в случае численного задания параметров.
3. Теорема о взаимосвязи решений задач Золотарева и полиномиальной трудоемка в применении. Основной проблемой является то, что для использования теоремы необходимо знать как расположение всех точек альтернанса, так и промежутки их изменения.
Заключение. В результате анализа решений задачи Золотарева и полиномиальной и сопоставления их промежутков альтернансности был получен вид решения второй задачи Золотарева с помощью полиномиальной задачи в зависимости от значения параметра Л.