1 Введение 4
2 Постановка задачи 7
3 Модель спектральной огибающей и её параметры 9
3.1 Расчёт коэффициентов линейного предсказания 9
3.2 Линейные спектральные пары и их свойства 10
3.3 Интерполяция LSP 16
4 Заключение 19
5 Список литературы 20
Большое количество подходов к моделированию и синтезу речевых сигналов было разработано в последние 50 лет [3, 4]. Большое распространение получили биомеханические модели Г. Фанта и Дж. Фланагана [5, 6, 7] и особенно параметрическая FL модель [8], выделяющая структуру импульса голосовых связок.
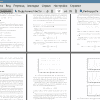
Рисунок 1.
Звуковой сигнал на выходе голосовых связок далее проходит через голосовой тракт, включающий шейный отдел, горло, рот и губы. Отражение от стенок этого тракта преобразуют выхлоп голосовых связок в конкретный звук (аллофон). Голосовой тракт моделируется линейной системой невысокого порядка. Таким образом, установление соответствия между аллофонами русского языка и параметрами линейных систем моделирования голосового тракта вполне достаточно для моделирования каждого аллофона. В задаче синтеза слитной речи к этой проблеме необходимо добавить гладкие переходы между аллофонами, а также просодические характеристики — интонацию, длительность, громкость.
Основным показателем линейной системы, моделирующей голосовой тракт и влияющей на восприятие аллофона, является спектральная огибающая — модуль передаточной функции линейной системы. На рис. 1 показаны типичные спектральные огибающие для звуков /о/, /е/ и /u/ (транскрипция латиницей).
Главную роль в спектральных огибающих играют небольшие промежутки частот, на которых значения функций относительно велики, или примерно окрестности локальных максимумов сглаженных огибающих. Эти промежутки называются формантами. Физиологам и фонетистам известно, что полный набор формант практически определяет восприятие звука человеком.
По традиции форманты указываются своими средними значениями в Гц. Поскольку каждый аллофон может быть произнесён даже одним человеком очень по-разному, а разными людьми совсем по-разному, но тем не менее быть правильно понятым всеми, то смещение форманты не всегда приводит к потере восприятия, и в действительности есть целый класс как спектральных огибающих, так и наборов формант, который воспринимается примерно, как один аллофон.
Наибольшее значение для восприятия имеют первая и вторая форманты по возрастанию частоты. В частности, для/a/ это обычно (650, 1150)Гц, для /o/ — (550, 850)Гц, для открытого /e/— (650, 1500)Гц , для /"/ - мягкого /e/ — (650, 2250)Гц , для /u/ — (360, 600)Гц.
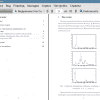
В международном фонетическом словаре все гласные всех языков расположены в виде трапеции (рис. 2), оси которой связаны с первой и второй формантой. В действительности, направление вверх трапеции указывает на степень раскрытия рта, а направление влево — на сколько выдвинут язык наружу.
Рисунок 2.
Хорошо разработанным в настоящее время является формантный синтез [9], который обезличен. Вырабатываются отдельные аллофоны, которые не привязаны к конкретному диктору.
В данной работе была поставлена другая задача. В результате специально проведённых сложных экспериментов были получены характеристики голосового тракта для нескольких гласных конкретного диктора. Требуется интерполировать эти данные на характеристики голосового тракта других гласных этого же диктора.
В работе был предложен новый подход к синтезу гласных для фиксированного диктора. Ключевыми моментами этого подхода является:
• Расчет спектральных огибающих и импульсных характеристик по записанным данным полученным из сложных экспериментов.
• Вычисление линейных спектральных пар по полученным спектральным огибающим.
• Интерполяция вектора линейных спектральных частот.
• Вычисление коэффициентов линейного предсказания из полученных LSP и синтез новых гласных.
Разработанный алгоритм гладкого движения формант обеспечивает синтез промежуточных гласных определенного диктора в соответствии с трапецией IPA. Кроме того было предложено новое доказательство важных для алгоритма свойств линейной спектральной пары. Алгоритм синтеза был реализован в математической среде MATLAB. Синтезированные промежуточные фонемы звучат четко и ясно. Такой метод может найти широкое применение в синтезе речи с фиксированным диктором.
