1 Введение 2
1.1 Общие определения 2
1.2 Местная группа и Местный поток 4
2 Описание использованного метода 7
2.1 Разделение выборки на членов группы и поток 7
2.2 Локальный коэффициент Хаббла 8
2.3 Локальная плотность темной энергии 9
2.4 Перенос начала координат к центру Местной группы 9
3 Диаграммы «скорость-расстояние» 11
3.1 Ближайшая Вселенная (1,5 - 12 Мпк) 11
3.2 Средняя Дистанция (12 - 200 Мпк) 15
3.3 Дальняя Вселенная (200 - 520 Мпк) 18
4 Заключение 22
Список литературы 23
1.1 Общие определения
Темная энергия - невидимая, идеально однородная космическая среда, заполняющая всё пространство с постоянной плотностью, физическая природа и структура которой неизвестны. Открыта в конце 1990-х годов с помощью космического телескопа «Хаббл» (HTS - Habble Space Telescope), по наблюдениям сверхновых типа 1а [1], [2]. Она характеризуется тем, что создаёт эффект антитяготения. Это явление хорошо описывается общей теорией относительности (ОТО), созданной А. Эйнштейном почти 100 лет назад [3].
В приближении ньютоновской механики, ОТО утверждает, что помимо всемирного закона тяготения Ньютона, подчиняющегося закону обратных квадратов:
(формула 1 в виде рисунка)
во Вселенной существует сила антитяготения с линейной зависимостью силы от расстояния:
(формула 2 в виде рисунка)
Здесь G - гравитационная постоянная, а рл - постоянная величина, являющаяся плотностью темной энергии. Эти силы противодействуют друг другу, следовательно имеют противоположные знаки. Формула (1) описывает движение «пробной» частицы малой массы m в поле тяжелой сферической массы М, R - расстояние от частицы до центра массы. Формула (2) описывает силу отталкивания между двумя частицами находящимися на расстоянии R. Не трудно заметить, что в отличии от Fn, которая создается массами самих тел, Fe от них не зависит и создается темной энергией. А так как Fe растет линейно с расстоянием, а Fy убывает, начиная с некоторого момента Fe станет больше Fy.
Плотность темной рл энергии выражается через космологическую постоянную Эйнштейна - Л [3]: рл = (с2Л)/(8лО). Массовая доля темной энергии измерена [4] с точностью до нескольких процентов Пл = (0.685 ± 0.013). Из неё легко получить плотность темной энергии рл, домножив Пл на критическу плотность рсгц = 0.961 х10-29 г/см3; рл = ПлPcrit = 0.663 х10-29 г/см3. Темная энергия доминирует по плотности в наблюдаемой Вселенной, ее доля составляет ~ 70% от полной. Представление об ан- тигравитирующей среде с постоянной плотностью стало общепринятым и лежит в основе современной стандартной космологической модели (ACDM - модель, CDM - аббр. от англ. Cold Dark Matter).
Одним из наиболее важных следствий открытия темной энергии, является доказательство ускоренного расширения Вселенной. Экспериментально расширение Вселенной проявляется в виде выполнения закона Хаббла в глобальном масштабе (здесь и далее глобальный масштаб - расстояния порядка 1 Гпк). Закон Хаббла устанавливает зависимость между расстоянием до галактики D и ее лучевой скоростью V, через коэффициент пропорциональности 110 - постоянную Хаббла. Эта величина определяет характерное время разбегания галактик. По последним оценкам сделанным космической обсерваторией Планк (Plank space observatory) [4] величина IF = (67.31 ± 0.96) км/с/Мпк.
Вскоре после открытия темной энергии было выдвинуто предположение о том, что создаваемое ей антитяготение способно проявить себя не только у края наблюдаемого мира, но и в ближней Вселенной [5], [6].
1.2 Местная группа и Местный поток
Глобальные космологические объёмы с поперечником в ~ 300 Мпк и более однородны по распределению галактик - это масштабы, в которых применима стандартная ACDM - модель. Локальная Вселенная устроена иначе, галактики в ней распределены по ближнему объёму крайне неоднородно. Подавляющее их число собранно в уплотнения, называемые группами (с размерами ~ 1 Мпк) и скоплениями (~ 10 Мпк), тогда как в пространстве между этими уплотнениями галактик очень мало.
Прежде всего рассмотрим Местную группу галактик. Её образуют галактики Млечный путь и галактика в Андромеде (M31) ео своими спутниками и другими, менее массивными, членами.
Местная группа - гравитационно связанная квазистационарная система с полной массой материи (барионной и темной) М = (2 Щ 3) х 1012М0, где М0 = 2 х 1033 г - масса Солнца. Радиус этой группы ~ 1 Мпк. Вне группы на расстоянии 1-3 Мпк от её центра наблюдаются карликовые галактики, все они, без исключения, движутся в направлении от группы, причём их лучевые скорости тем больше, чем больше расстояние от её центра. Это местный поток разбегания галактик.
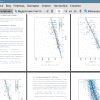
Каждая из галактик группы и потока детально изучена по наблюдениям с помощью HST и других крупных инструментов [7]. С хорошей точностью до 10% - измерены расстояния до галактик Местной группы и потока вокруг нее, скорости галактик измерены с точностью не хуже 5-10 км/с. Результаты наблюдений представлены на диаграмме скорость - расстояние (рис. 1), воспроизведенной из работы И. Д. Караченцева и др. [8] по наблюдательным данным полученным из каталога Catalog & Atlas of the LV galaxies [8] составленного И. Д. Караченцевым и его командой.
При построении данной диаграммы лучевые скорости были исправлены за движение Солнца относительно центра Местной группы, а расстояния, измеренные до цента нашей галактики, пересчитаны на расстояния до центра Местной группы. Использовались данные по 247 галактикам, расстояния до которых получены преимущественно высокоточными методами. В ней рассматривается поле скоростей Vlg < 500 км/с на расстоянии 8 Мпк. В целях сохранения точности, члены Местной группы убраны с диаграммы, а начало потока принято равным 1.5 Мпк. Линия регрессии Vlg = HD^g, проведенная через начало координат, соответствует локальному значению «постоянной» Хаббла Н0 = (61.3 ± 6.4) км/с/Мпк.
Эта оценка, в пределах погрешности измерения скорости и расстояния, хорошо коррелирует с значением глобальной постоянной Хаббла.
Возникает справедливый вопрос: А повторится ли картина на большем масштабе? В данной работе будут представлены диаграммы локальных потоков с полем скоростей до 30000 км/с на расстоянии до 520 Мпк и результаты исследования локальных значений коэффициента Хаббла, полученные на основе этих диаграмм. Будет показано, что в пределах погрешности измерений, локальные коэффициенты Хаббла можно считать равными глобальной постоянной Хаббла.
Рис. 1.
В итоге проделанной работы было установлено, что поток разбегающихся галактик подчиняется линейному закону, схожему с законом Хаббла. Коэффициент пропорциональности в этом законе не отличается от глобальной постоянной Хаббла, более чем на ошибку измерения лучевых скоростей и расстояний до членов потока.
По локальным коэффициентам Хаббла были получены локальные плотности темной энергии, их отличие от глобально значения плотности темной энергии, так же как и сами коэффициенты Хаббла, не превосходите величины ошибки наблюдательных данных.
В следствии выше перечисленного, можно сделать вывод, что природа локальных потоков схожа с природой глобальных. Так как и те и другие ускоряются антигравитационным воздействием уникального космологического феномена - темной энергией.
