1 Введение 1
1.1 Постановка задачи 1
2 Математическая модель многокомпонентного реагирующего газа 3
2.1 Выбор численного метода 3
2.2 Основные газодинамические уравнения 3
2.3 Осреднение по Фавру 6
2.4 Модель турбулентности Спаларта-Аллмареса 7
2.5 Уравнение диффузий 9
2.6 5-ти компонентный реагирующий воздух 11
3 Результаты и обсуждения 13
3.1 Результаты при значении M = 12 13
3.2 Сравнение с экспериментальными данными и моделью совершенного газа 18
4 Заключение 20
5 Благодарности 21
Основными особенностями гиперзвуковых течений является значительный рост температуры за фронтом головной ударной волны, сильное торможение потока внутри ударного слоя и аэродинамический нагрев поверхности. Сложность явлений, сопровождающих полет гиперзвуковых летательных аппаратов, практически исключает возможность полного моделирования условий натурного обтекания в ударных трубах, в связи с чем методы математического моделирования приобретают важной значение. Численное моделирование гиперзвуковых течений связано с использованием сложной математической модели, включающей уравнения, описывающие пространственное течение вязкого сжимаемого газа, уравнения модели турбулентности, уравнения состояния, уравнения химической кинетики.
В данной работе обсуждается построение и реализация математической модели, предназначенной для численного моделирования гиперзвукового обтекания сферы с учетом неравновесных физико-химических процессов, протекающих в высокотемпературном воздухе. Основной целью работы является построение графика зависимости безразмерной толщины ударного слоя от числа Маха на основе данных, полученных в результате численного расчета, и сравнение данного результата с экспериментом [2].
1.1 Постановка задачи
Сфера c диаметром 1,27 см обтекается гиперзвуковым потоком. В рамках дипломной работы стоит задача рассмотреть данный процесс при числах Маха от 8 до 20 с шагом 0,5. Статическое давление на входе считаем равным 666,61 Па, статическая температура на входе равна 293 К. Концентрация двухатомного азота равна 76,7 %, концентрация двухатомного кислорода составляет 23,3 %.
Средняя длина свободного пробег молекул воздуха в условиях рассматриваемой задачи составляет([ Л ] = м ):
Л = ^bT к 4, 89 • 10 1
у2%ар
kb - постоянная Больцмана, а - эффективное сечение молекулы N2.
Число Кнудсена в данной задаче принимает значение:
Кп = « 0, 008
^sph
Так как Кп ^ 1 система уравнений Навье-Стокса применима для решения этой задачи.
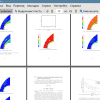
Схема расчетной области приводится на Рис.1. Внешняя граница расчетной области удалена от сферы на 4 мм в точке торможения и на 8.65 мм в верхней точке. Задача решается в осесимметричной постановке. На входной границе задаются граничные условия сверхзвукового втекания в расчетную область, а на выходной границе — условия сверхзвукового вытекания. На стенке используются граничные условия прилипания, но для упрощения постановки выходного граничного условия в конце сферы небольшой участок стенки задается как не вязкая стенка с проскальзыванием. Поверхность сферы полагается теплоизолированной. Расчетная сетка состоит из 400 х 400 = 160000 гексагональных ячеек.
Рис. 1: Схема расчетной области
Для численного расчёта данной задачи будем использовать программный модуль Ansys Fluent.
В данной работе был произведен расчет гиперзвукового обтекания сферы при числах Маха от 8 до 20 с шагом 0.5 с помощью программного комплекса Ansys Fluent. Была исследована математическая модель, включающая в себя уравнения течения вязкого сжимаемого газа, осредненью по Фавру, модель турбулентности Спаларта-Аллмареса, уравнение состояния и уравнения неравновесной химической кинетики. За газовую среду был взят пятикомпонентный реагирующий воздух N2,02, NO, N, О, химические процессы описаны неравновесной однотемпературной моделью с кинетической схемой Парка.
На основе результатов были построены поля распределения газодинамических параметров течения, концентраций компонентов и график зависимости давления от расстояния до поверхности сферы при числе Маха 12. Главным результатом работы является график зависимости безразмерной толщины ударного слоя от числа Маха. На этом графике проведено сравнение результатов расчетов на основе нашей модели, результатов расчета этой задачи при модели совершенного нереагирующего газа, результатов при использовании модели равновесной химической кинетики Крайко [7], а также результатов эксперимента [2]. По этому графику видно, что наша модель дает хорошее совпадение итоговых результатов, а небольшие расхождения могут быть обусловлены простотой модели газовой среды.
