1 Введение 2
2 Эффект Зеемана 2
3 Метод А-ДКБ 4
3.1 Четность состояния 5
4 Линейный и квадратичный вклады в эффект Зеемана 7
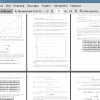
4.1 Численное дифференцирование 9
4.2 Результаты 12
5 Эффект Зеемана для уровней сверхтонкой структуры 13
5.1 Общие сведения 13
5.2 Вычисление поправки к g-фактору на сверхтонкое расщепление 15
5.3 Формула Брейта-Раби 17
6 Заключение 19
7 Приложение 19
Список литературы 22
Многозарядные ионы — это относительно простая система для теоретических расчетов, что позволяет получить результаты с высокой точностью. Сравнение теоретических и экспериментальных значений g-фактора позволяет с высокой точностью получить значения фундаментальных констант. Высокоточные измерения g-фактора были выполнены для водородоподобных ионов углерода [1, 2], кислорода [3] и кремния [4, 5]. Последнее наиболее точное измерение для водородоподобного углерода позволило определить массу электрона с рекордной точностью [6]. Кроме того, были выполнены аналогичные эксперименты для литиеподобных ионов кремния [7] и кальция [8].
Все описанные выше экспериментальные данные находятся в прекрасном согласии с теоретическими значениями. Среди наиболее существенных теоретических достижений по g-фактору водородоподобных ионов можно отметить работы [9, 10, 11, 12, 13, 14, 15]. Наиболее точные расчёты для литиеподобных ионов были выполнены в работах [16, 17, 18, 19, 20]. Более полный обзор по этой тематике можно найти, например, в работе [21].
Как показано в работах [22, 23] исследования g-фактора водородо-, литие- и бороподобных ионов в различных комбинациях позволят независимо определить постоянную тонкой структуры а при достижении необходимой точности как в теории, так и в эксперименте. Первым высокоточным экспериментом для бороподобных ионов должно стать измерение зеемановского расщепления в бороподобном аргоне, которое готовится в настоящее время в GSI. Как показано в работе [24], в этом случае существенную роль играют нелинейные по магнитному полю эффекты. В работах [25, 26] получены наиболее точные на сегодня значения g-фактора, а также квадратичного и кубического вкладов в эффект Зеемана для бороподобного аргона.
Изучение эффекта Зеемана для уровней сверхтонкой структуры позволяет также с значительной точностью определить магнитный момент ядра. В работе [27] предложена схема соответствующего эксперимента. Теоретические расчёты различных поправок были выполнены в работах [28, 29, 30] для водородоподобных ионов и в работе [31] для литиеподобных ионов. Высокоточное определение магнитных моментов ядер важно как для атомной спектроскопии, так и для тестирования различных моделей в ядерной физике.
Метод А-ДКБ [32] позволяет учесть магнитное поле вместе с полем ядра в нулевом приближении, что дает возможность более точного определения вкладов в g-фактор и упрощения расчетов, по сравнению с теорией возмущений.
В данной работе были вычислены линейный и квадратичный вклады в эффект Зеемана для состояний 1s, 2s, 2р 1,2pз, имеется хорошая сходимость с расчетом по теории возмущений. Получены формулы для матричных элементов на волновых функциях в присутствии магнитного поля для различных одноэлектронных и двуэлектронных операторов. Вычислена поправка к g-фактору водородоподобного иона на сверхтонкое расщепление. Результаты для состояний 1s, 2s согласуются с уже опубликованными. Результаты для состояний 2р 1,2рз являются новыми. В дальнейшем, с использованием развитого метода, планируется воспроизвести и уточнить формулу Брейта-Раби, описывающую зеемановское расщепление уровней сверхтонкой структуры в произвольном магнитном поле.
