О нестандартном задании характеристической функции в кооперативных играх

Введение 4
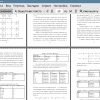
Постановка задачи 7
Обзор литературы 9
1 Стандартное построение характеристической функции в коопе­ративных играх 10
1.1. Понятие характеристической функции 10
1.2. а - характеристическая функция 10
1.3. Пример построения а - характеристической функции 11
2 Нестандартное построение характеристической функции 13
2.1. 6 - характеристическая функция 13
2.2. Игра с отрицательными связями 13
2.3. Пример построения 6 - характеристической функции 14
2.4. Пример с квадратичной функцией полезности 20
2.5. Пример с логарифмической функцией полезности 21
3 ( - характеристическая функция 22
3.1. Определение 22
3.2. Супераддитивность 23
3.3. Пример с квадратичной функцией полезности 23
3.4. Пример с логарифмической функцией полезности 24
3.5. Кооперативная игра управления вредными выбросами на при­мере предприятий Иркутской области 26
Выводы 32
Заключение 33
Приложения 36
3.6. Приложение 1. Доказательство супераддитивности а - харак­теристической функции для Примера 1 36
3.7. Приложение 2. Доказательство супераддитивности 5 - харак­теристической функции для примеров 38
3.7.. 1 Пример 1 38
3.7.. 2 Пример 3 40
3.8. Приложение 3. Доказательство супераддитивности ( - харак­теристической функции для примеров 44
3.8.. 1 Пример 1 44
3.8.. 2 Пример 3 46
3.9. Приложение 4. Вычисления и программный код для практи­ческой задачи 48
3.9.. 1 Вычисление штрафов 48
3.9.. 2 Программный код 50
Купить

Теория игр представляет собой набор математических инструментов, с помощью которых можно выяснить природу конфликта и его управление. Первоначально теория игр находила свое применение в рамках экономи­ческой науки, но позднее также получила широкое признание и в других социальных науках. Сегодня теория игр применима к широкому диапазону поведенческих отношений, и в настоящее время является общим термином для науки логического принятия решений. Теория игр актуальна и находит свое применение в экономике (рынок игр, торги, аукционы, совместное рас­пределение затрат), политике (голосование), окружающей среде (природе) (рыболовство, борьба с загрязнением), промышленности (телекоммуника­ции, проблемы местоположения, заключение контрактов и т.д.) и других областях.
Существует большое количество классов игр [1,2], однако выделяют две основные ветви теории игр: некооперативные и кооперативные, кото­рые значительно отличаются друг от друга областью решаемых задач. В некооперативной теории игр рассматривается в основном то, как интеллек­туальные индивиды взаимодействуют между собой для достижения соб­ственных целей. У каждого игрока имеется задача выбора стратегии, мак­симизирующей выигрыш этого игрока, который, в свою очередь, зависит от стратегий, выбранных другими игроками. Игра называется кооперативной (коалиционной), если игроки могут объединяться в группы и действовать в соответствие с некоторым заранее определенным принципом оптималь­ности, который включает в себя соглашения о множестве кооперативных стратегий и механизм распределения общего выигрыша между игроками. Кооперация является одной из основных форм человеческого поведения.
Большинство кооперативных игр описываются с помощью характери­стической функции, а вопрос построения данной функции является одним из основных в теории указанных игр. Как известно, существуют различ­ные способы задания характеристической функции, наиболее известными и часто используемыми являются так называемые а, Д у и 5 - характе­ристические функции [3,4]. Однако в данной работе также предлагается рассмотреть новый способ для построения характеристических функций в кооперативных играх — ^-характеристическую функцию. Согласно новому подходу характеристическая функция вычисляется в два этапа с использова­нием выражений для оптимальных управлений, что существенно упроща­ет процесс вычислений по сравнению с построением характеристической функции Неймана-Моргенштерна.
Очень важными с точки зрения практического применения являют­ся теоретико-игровые задачи в области природоохранного менеджмента, а особенно, кооперативные игры управления вредными выбросами. Загряз­няющие вещества, поступающие в атмосферный воздух, являются факто­ром, воздействующим на самые разные процессы и объекты, в том числе, на климат. В Париже на 21-й сессии Конференции Сторон Рамочной кон­венции ООН об изменении климата, которая состоялась 12 декабря 2 года, был подписан документ, в котором, в частности, указывается, что в период до 2020 года развивающиеся страны получат 100 млрд долларов в год для решения проблем климата [5]. Во избежание данных проблем необходима заинтересованность правительства в сфере охраны окружающей среды.
Работа имеет следующую структуру. Глава 1 содержит общие сведе­ния о кооперативных играх, также вводится определение о характеристической функции (классический способ построения характеристической функции) и рассматривается пример с конкретным видом функции полезно сти.
В Главе 2 описана ^-характеристическая функция, которая впервые была предложена в работе [6]. При построении данной функции, в отли­чие от подхода [4] учитываются ограничения на управления и проверяется выполнение условия супераддитивности характеристической функции для примеров. Выяснилось, что при заданных ограничениях ^-характеристическая функция не супераддитивна в общем случае, приведен контрпример.
В Главе 3 новая характеристическая функция, построенная нестан­дартным образом в работе [7], адаптирована на случай игры, описанной в Главе 1. Доказана супераддитивность рассмотренной функции в общем случае. Теоретический результат продемонстрирован на примерах. В конце работы приводится пример построения характеристической функции всеми тремя изученными способами, основанный на реальных данных об очистке и загрязнении окружающей среды тремя предприятиями Иркутской обла­сти. Данная проблема сформулирована как кооперативная игра трех лиц. В качестве кооперативного решения вычислен вектор Шепли для всех трех способов построения характеристической функции.
Купить