Введение 3
Постановка задачи 10
Проблематика и обзор литературы 10
1 Описание экспериментов 14
1.1 Выбор нейронной сети, алгоритма обучения и других пара­метров 15
1.2 Выбор метрик 19
2 Программная реализация, тестирование и анализ результа­тов 22
2.1 Инфраструктура 22
2.2 Результаты тестирования, выбор метрик 23
2.3 Эволюция выбранных параметров во время обучения 25
2.4 Анализ результатов 27
3 Применение разработанных критериев и перспективы 30
3.1 Динамическое расширение слоя 31
3.2 Многослойные сети 31
Заключение 33
Литература 35
Купить

В последние годы наблюдается активной рост интереса к искусствен­ным нейронным сетям (ИНС) как к методу решения многих практических задач. Этот интерес связан с разработкой новых архитектур и методов обучения, которые позволили преодолеть основные проблемы ИНС и зна­чительно расширить круг решаемых ими задач. Также актуальность иссле­дований нейронных сетей дополняется стремительным увеличением вычис­лительных мощностей, доступных исследователям, а в частности распро­странением графических процессоров, которые в последнее время стали основным средством для обучения сложных ИНС.
Такие авторы как Джеффри Хинтон и Ян Лекун своими работами (например, [1, 2]) внесли большой вклад в процесс выхода нейросетевых исследований из зимы (период с 1990 по 2010 гг. [3]). Описанные в этих и последующих работах методы позволили обучать действительно глубо­кие нейронные сети (ранее ИНС с 8 слоями считалась очень глубокой, в то время как современная сеть ResNET использует 150 слоев [4], и это не предел) для более глубокого анализа информации. Также стало возмож­но эффективное обучение рекуррентных ИНС, позволяющих обрабатывать временные ряды данных (например аудио, видео, тексты).
Столь стремительное расширение возможностей нейронных сетей тре­бует проведения дополнительных исследований по выявлению применимо­сти данного подхода к той или иной задаче, разработке новых архитектур и преодолению существующих ограничений. Подобные исследования поз­волят эффективно использовать столь мощный инструмент как ИНС и предотвратить наступление еще одного периода застоя.
Одной из важнейших проблем, возникающих при проектировании ИНС, является выбор ее архитектуры (глубина, ширина, тип слоев нейро­нов). Для каждой задачи требуется индивидуальный подход, и часто выбор архитектуры сводится к обучению множества нейронных сетей с различ­ной архитектурой в поисках оптимальной. Поскольку обучение даже одной нейронной сети является вычислительно дорогим (требуется оптимизация градиентными методами до миллиарда параметров), такой перебор пред­ставляется очень неэффективным. В рамках данной работы проводится исследование и разработка методов для оптимизации выбора количества нейронов в полносвязном слое ИНС.
Введение в теорию искусственных нейронных сетей
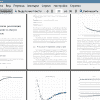
Исследование искусственных нейронных сетей началось с работ У. Мак- каллока и У. Питса на стыке нейробиологии и математики [5], в кото­рых они предложили математическую модель биологического нейрона как взвешенного порогового сумматора входных сигналов. Нейрон такого ти­па изображен на рисунке 1, и результат его работы можно представить в виде y = F(X • w), где x = (x1, x2,..., xn) — вектор входных сигналов, w = (w1,w2, ...,wn) — строка-вектор весовых коэффициентов, F : R ! R — функция нелинейного преобразования. Функцию F принято называть активационной, и в случае нейрона Маккаллока-Питса она равна
I 1, если x > 0;
F (z ) =
I 0, если x <= 0
Рис 1. Математическая модель нейрона Маккаллока-Питса.
Позже были разработаны и другие модели, более точно повторяющие свойства нейронов, но именно простые модели типа Маккаллока-Питса с некоторыми изменениями до сих пор широко используются в ИНС. При правильном выборе весовых коэффициентов нейрон такого типа может ис­пользоваться для линейного разделения n-мерного пространства, а объ­единение нескольких нейронов (путем подачи выхода одного нейрона на вход другого) может использоваться в задачах классификации и аппрок­симации. Итерационный процесс выбора весовых коэффициентов (оптими­зации) принято называть обучением.
На сегодняшний день наиболее распространена следующая модель нейрона:
y = F (X • w + b), (2)
не сильно отличающаяся от модели Маккаллока-Питса. Здесь b — дополни­тельное смещение (bias) полученной суммы, которое применяется в неко­торых задачах. b не является фиксированным параметром и также подвер­гается оптимизации при обучении. В качестве активационной функции F на данный момент распространены:
• функции сигмоидального типа (сглаженные пороговые). В качестве та­кой функции часто применяется
F (z) = ■.) = —1-; (3)
-L I —
и гиперболический тангенс;
• функции типа ReLU (rectified linear unit). За основу таких функций взята F(z) = max(0, z), к которой могут применяться различные мо­дификации: сглаженный ReLU F(z) = log(1 + exp(z)), ReLU с утечкой F(z) = max(z,az),a < 1 и другие;
• в задачах классификации распространено использование функции softmax
-zi
Fi(zi,z2,...,zK) = —^ ,i = 1,2,...,K (4)
Ek=i -
для сравнения выходов K нейронов. В результате применения softmax выходы всех участвующих нейронов находятся в интервале от 0 до 1, а их сумма равна 1. Использование такой активационной функции явля­ется расширением описанной модели нейрона, так как подразумевает взаимную зависимость выходов нескольких нейронов.
Столь простые вычислительные элементы как нейроны могут давать интересные результаты при объединении их в сети и применении различ­ных алгоритмов обучения. Первой нейронной сетью, которая могла распо­знавать визуальные образы стал перцептрон Розенблата [6], изображенный на рисунке 2.
Рис. 2. Однослойный перцептрон Розенблата со многими выходами [7].
Со времен этой нейронной сети было разработано множество методов соединения нейронов в сети, среди которых можно выделить два класса: сети прямого распространения и сети, имеющие обратные связи (рекур­рентные). В процессе прохождения сигнала от входа сети прямого распро­странения к выходу, каждый нейрон производит вычисления только один раз. Пример такой ИНС приведен на рисунке 3.
Рис. 3. Архитектурный граф многослойного персептрона с двумя скрытыми слоями [8].
В рекуррентных нейронных сетях сигнал может образовывать циклы, проходя несколько раз через один нейрон. На рисунке 4 приведен пример сложной рекуррентной нейронной сети АРТ со множественными обратными связями [9]. Для простоты в данной работе будут рассматриваться толь­ко нейронные сети прямого распространения, однако рекуррентные также очень эффективны в некоторых задачах и широко используются [11, 12].
Рис. 4. Схема нейронной сети с обратными связями АРТ-1 [10].
Еще одним широко распространенным приемом упрощения нейрон­ных сетей является объединение схожих нейронов в группы. В частности, если несколько нейронов имеют одно множество входных сигналов и одну активационную функцию, такую группу называют нейронным слоем. Ре­зультат работы слоя из m нейронов можно представить в виде матричного умножения
У[т] F(x[n] ' W[mxn])- (5)
Здесь y = (у1;У2; ...yym) — выходной вектор-строка, элементами которой являются выходы нейронов, входящих в слой; W = (wi,W2, ...,wm)T — ве­совая матрица, строками которой являются весовые вектор-строки входя­щих в слой нейронов; F(У) = (F(z1),F(z2),...,F(zm)) — функция отобра­жающая F : Rm ! Rm путем поэлементного применения одной скаляр­ной функции F к каждому элементу аргумента; для удобства размерности векторов и матриц приведены в квадратных скобках. Вычисленный таким образом выход у передается на вход следующему слою. Матричный под­ход широко используется в ИНС, поскольку облегчает вычисления, ана­лиз и проектирование нейронных сетей. Благодаря этим преимуществам объединение нейронов в слои получило очень широкое распространение и применяется практически во всех современных ИНС (как прямого распро­странения, так и рекуррентных).
Использование концепции нейронных слоев позволяет перейти от ней­рона как элементарной единицы нейронной сети к нейронному слою как основному структурному элементу. Таким образом, проектирование архи­тектуры нейронной сети прямого распространения сводится к выбору ко­личества последовательно идущих слоев (глубина), количества нейронов в каждом слое (ширина слоя) и типа слоя. Например, могут использоваться следующие типы слоев:
• может варьироваться активационная функция слоя;
• при обработке изображений применяются сверточные слои. Основной идеей является использование общих весов для нескольких нейронов и выборочная связность нейронов с предыдущим слоем (в отличии от обычных, полносвязных слоев, в которых каждая компонента входного вектора подается на каждый нейрон слоя);
• вспомогательные слои, в которых вместо нейронов используется ал­горитмическое преобразование входного вектора. Примерами являют­ся слои нормализации, сокращения размерности (subsampling) и слой добавления шума (dropout). Использование таких модулей позволяет решить ряд существенных проблем, возникающих при обучении ней­ронной сети.
Примером сложной ИНС является GoogLeNet [13], схема которой приведе­на на рисунке 5. Эта нейронная сеть является одной из лучших в задаче классификации изображений и, несмотря на значительную сложность при­веденного графа, полностью состоит из описанных выше слоев.
Рис. 5. Граф глубокой нейронной сети GoogLeNet [13].
Существуют различные подходы к классификации слоев нейронной сети. В данной работе будут использоваться следующие определения:
• вектор, который подлежит обработке нейронной сетью и подается на вход первому нейронному слою, обозначим как входной вектор;
• нейронный слой, стоящий в конце сети прямого распространения, выхо­дом которого является результат обработки всей нейронной сети, обо­значим как выходной слой;
• все нейронные слои, которые стоят перед выходным слоем, будем на­зывать скрытыми.
Классической задачей, в которой нейронные сети превзошли дру­гие алгоритмы, является распознавание рукописных цифр. Для настройки и сопоставления методов распознавания изображений Национальным ин­ститутом стандартов и технологий США была составлена выборка руко­писных цифр из 70000 изображений в градациях серого размером 28*28 пикселей [14]. В данной задаче наилучший результат показал ансамбль из нескольких нейронных сетей с ошибкой 0.23% неверно классифициро­ванных изображений [15]. Для сравнения, лучший результат без исполь­зования нейронных сетей показал метод k ближайших соседей с размером ошибки 0.52%.
Купить