Содержание 2
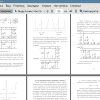
Введение 3
Постановка задачи 7
Обзор литературы 8
Глава 1. Устойчивость классических методов Рунге — Кутты 9
1.1. Тестовое уравнение Далквиста 10
1.2. Сведение системы к одному уравнению 11
1.3. Примеры функций устойчивости явных методов 13
Глава 2. Перекрёстная система 15
2.1. Уравнения второго порядка и устойчивость методов Рунге — Кутты — Нюстрёма 16
2.2. Равносильная перекрёстная система 17
2.2.1. Устойчивость при чисто мнимых Л 18
2.2.2. Альтернативный подход к определению устойчивости 25
2.3. Сведение к случаю равных элементов 29
2.4. Сведение блочно-перекрёстной системы к простейшей матрице 31
Глава 3. Система 0J 38
3.1. Простейшая система 0J 39
3.2. Сведение системы из двух уравнений к простейшей 41
3.3. Блочная система 43
Выводы 44
Заключение 45
Список литературы 47
Купить

В истории развития классических методов численного решения обыкновенных дифференциальных уравнений (ОДУ), таких как методы Рунге — Кутты (РК), экстраполяции, Адамса, изначально разработанных для ручного счета, наблюдается постоянное расширение классов решаемых задач, обусловленное технологическим развитием машинного счета. Мощности ЭВМ непрестанно росли, что давало ещё больше возможностей для решения более трудных и сложных задач. С новыми задачами стали появляться и новые трудности, связанные с аппроксимацией и устойчивостью более эффективных и надежных алгоритмов численного интегрирования систем обыкновенных дифференциальных уравнений (СОДУ).
Отсутствие однородности в реальных задачах, состоящее в том, что встречаются задачи не исключительно жесткого или нежесткого типов, а почти всегда их сочетание, явилось важным мотивом для усовершенствования и развития численных методов решения жестких и нежестких типов задач.
Классический подход к распространению методов решения скалярных уравнений на системы заключается в формальной подстановке векторов в расчётные схемы. Однако, возможен другой способ, при котором для разных компонентов вектора неизвестных функций применяются разные расчётные схемы. Такие методы, которые называют многосхемными, получили применение при решении так называемых разделяющихся СОДУ, в которых выделяют, например, жёсткую и нежёсткую части и решают их по-разному. В настоящее время многосхемные методы используют в том числе в построениях симплектических решателей, для решения уравнений в частных производных, для лучшего отслеживания быстрых и медленных процессов в сложных системах и т. д.
В общем виде явный метод Рунге — Кутты численного интегрирования разделяющейся СОДУ
^Узг fчп л
= fs(x>yo>->Уп)>s = 0,1,... ,п,
ах
ys(x0) = ys0,s — 0,1,...,п,
xE[X0,Xk]^R,ys^[Xo,Xk]^R,
fs:[Xo,Xk]xRn+1^R, s — 0,1... , п,
выглядит следующим образом:
ms
ys(X + Ю * Zs— ys(x) + ^ bsJtscM,ш=1
где функция kso) — kso) (h) вычисляется по схеме
ш-1
ksuhfs(X + CSMk, yo(X) +’ &soj0gk0g’ ■■■ ,yn(X) +’ &smngkng')’
9=1g=i
Cs10,^stetl0,t 0Д, ■■■ , п,
а ys(x + h),zs - являются точным и приближенным значениями -й компоненты в точке х + h Е [X0,Xfc] соответственно, h - шаг метода.
Мы рассматриваем структурные методы [4] с целью минимизации числа этапов интегрирования, для повышения быстродействия, в случае, когда структурные особенности системы это позволяют. Во многих случаях при интегрировании СОДУ можно произвести разделение по структурным признакам. Так, например, один из вариантов такой структурной классификации подразумевает выделение трёх классов разделенных структурно выраженных систем.
Класс ЭД(п) - системы разделяющихся ОДУ с перекрестной структурой связей:
У'1 = fA+yJ,
У] = fj(x,yj-1)> j = 2,...,n,
здесь ys,fs - функции размерности rs. Необходимость в интегрировании систем класс ЭД(2) = ЭД(п), при п = 2
У1 = fi(x,y2),
У2 = f2(x,yi),
возникает достаточно часто в задачах моделирования механических и физических систем, управления и оптимизации. Так же, этому классу принадлежат и система ОДУ, полученная в результате сведения СДУ второго порядка, правая часть которых не зависит от первой производной. К примеру, задача небесной механики - задача двух тел. [4]
Системы класса ЭД(п), при п > 3, на практике встречаются реже. К примеру, задача классического оптимального линейного быстродействия или дифференциальное уравнение п — го порядка yn = f(x,y).
Второй класс - ® (системы структурно разделяющихся ОДУ):
y/ =fi(x,yi,^ ,yi-i,yi+i,^ ,yn), i = 1,^ ,1,
yj = fj(x,yi,... ,yi-i,yj-i), j = 1 + 1,... ,n,
где ys,fs - функции размерности rs.
Явный одношаговый метод типа Рунге — Кутты, ориентированный на интегрирование систем класса ®, носит название метода класса ®.
Последний класс - & (системы структурно разделяющихся ОДУ общего вида):
У'о = fo(x,yo,yi,- ,уп),
yl = fi(x,yi,- ,yi-lfyi+1,^ ,Уп) i = 1,- ,l,
y'i = fj(x,yi, ... ,yi-i,yj-i), j = l + 1, - ,n,
I e {0} и N, n e {0} и N, I < n,
x e [Xo,Xk] c R,ys: [%0,Xk] ^ R% s = 0,1........n,
i:.X-o.X:• R! --’'■> Rr. i = 1........................1,
fj- Wfc] ^ Rr~-"o-ir« ^ Rr>,j = l + 1.........n, ro> 0
Необходимость в интегрировании систем класса & возникает, например, в задачах различных систем ускорения и транспортировки пучков заряженных частиц. [4]
Явный одношаговый метод типа Рунге — Кутты, ориентированный на интегрирование систем класса &, носит название метода класса &.
Стоит отметить, что любой из методов класса & может быть использован для интегрирования систем классов ЭД(п) и ®, а любой из методов класса ® - для интегрирования систем класса ЭД(п).
Купить