Аннотация 2
Введение 6
1 Обзор существующих методов определения изоморфизма графов 8
1.1 Общие понятия изоморфизма графов и постановка задачи на исследование 8
1.2 Обзор основных алгоритмов перебора, решающих задачу определения изоморфизма графов 10
1.2.1 Алгоритм Ульмана 10
1.2.2 Алгоритм VF2 12
1.2.3 Алгоритм полиномиального времени 14
1.3 Обзор основных инвариантов графа 25
1.3.1 Вектор степеней вершин графа 26
1.3.2 Индекс Винера 28
1.3.3 Индекс Рандича 30
1.3.4 Диаметр графа 30
1.3.5 Число компонент связности 31
1.3.6 Хроматическое число 31
1.3.7 Определитель матрицы смежности 33
1.3.8 Упорядоченный вектор собственных чисел матрицы смежности 36
2 Программная реализация методов определения изоморфизма графов 40
2.1 Структура программы 40
2.2 Реализация вычисления инвариантов 42
2.3 Реализация алгоритма полиномиального времени 45
2.4 Пользовательский интерфейс приложения 46
3 Анализ полученных результатов 49
3.1 Формат проводимых экспериментов 49
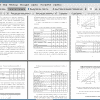
3.2 Результаты экспериментов 50
3.3 Сравнение инвариантов графа 54
Заключение 57
Список используемой литературы 59
Приложение А Иллюстрационный материал к выпускной квалификационной работе 61
В настоящее время необходимость проверки графов на изоморфизм возникает в различных областях исследований в таких направлениях как:
• компьютерная химия при решении химических задач с применением представления молекул в виде графов;
• автоматизация проектирования электронных схем при верификации различных их представлений в процессе проектирования микросхем;
• оптимизация программ при выявлении общих подвыражений;
• транспортная логистика при проектировании транспортных маршрутов;
• распознавание образов изображений при построении эталонного графа на основании информации о классе, к которому было отнесено исследуемое изображение, с которым будет производиться сравнение последующих создаваемых графов.
Выше представлены только некоторые области исследований, где вопрос распознавания изоморфизма графов возникает наиболее часто, но существуют также и другие сферы, использующие при решении своих задач графы, а, следовательно, в них так же может возникнуть необходимость распознавания изоморфизма графов. В связи с этим возрастает актуальность решения данной задачи.
В настоящее время существует два подхода к решению данной задачи - задачи определения изоморфизма графов [6]:
• перебор всех возможных комбинаций перестановок вершин графов с целью выявления совпадающей для обоих графов, что будет свидетельствовать об изоморфизме графов;
• отыскание полного инварианта графа, из совпадения значения которого однозначно бы следовало совпадение графов, то есть их изоморфность.
Объектом исследования в данной выпускной работе является задача определения изоморфизма графов.
Предметом исследования - инварианты графа.
Поскольку полного инварианта, вычислимого за полиномиальное время, на сегодняшний день не существует [6], целью данной выпускной квалификационной работы является исследование известных инвариантов графа [14] с целью выявления наиболее полного для решения задачи определения изоморфизма графов заданного типа.
Для достижения поставленной цели в рамках данной выпускной квалификационной работы необходимо решить следующие задачи:
1. Рассмотреть существующие алгоритмы решения задачи определения изоморфизма графов;
2. Рассмотреть существующие инварианты графов;
3. Реализовать один из известных алгоритмов перебора, выполняющий проверку графов на изоморфизм на языке программирования Java;
4. Реализовать вычисление инвариантов графа на языке программирования Java;
5. Провести эксперименты и анализ полученных результатов;
6. Выявить наиболее полный инвариант.
Данная выпускная квалификационная работа состоит из введения, трёх глав и заключения.
В первой главе представлено описание задачи определения изоморфизма графов, обзор существующих алгоритмов перебора и инвариантов графа.
Во второй главе описана программная реализация генерации графов, вычисления его инвариантов и одного из выбранных алгоритмов перебора.
В третьей главе представлены результаты экспериментов и их сравнительный анализ.
В ходе выполнения выпускной квалификационной работы было проведено исследование, объектом которого являлась задача определения изоморфизма графов с применением подхода, заключающегося в отыскании наиболее полного инварианта, из совпадения которого следовал бы изоморфизм графов. Были реализованы на языке Java алгоритм полиномиального времени и вычисление таких инвариантов, как:
• вектор степеней вершин графа;
• индекс Виннера;
• индекс Рандича;
• диаметр графа;
• число компонент связности;
• хроматическое число;
• определитель матрицы смежности;
• вектор собственных чисел матрицы смежности.
В ходе работы были выполнены следующие задачи:
1. Рассмотрены существующие алгоритмы решения задачи определения изоморфизма графов;
2. Рассмотрены инварианты графов;
3. Реализован алгоритм полиномиального времени, относящийся к группе методов, основанных на полном переборе и его модификациях, при решении задачи определения изоморфизма графов;
4. Реализованы вычисления инвариантов;
5. Реализован автоматизированный подход к проведению экспериментов, заключающийся в объединении процесса генерации графов с заданными параметрами и проведения проверки их на изоморфизм;
6. Проведены эксперименты и анализ полученных результатов.
Согласно анализу, наиболее полным инвариантом при определении изоморфизма графов описанного в представленной работе вида является вектор собственных чисел матрицы смежности. Показатели, свидетельствующие о наименьшей эффективности применения инварианта при определении изоморфизма графов, были зафиксированы у числа компонент связности, диаметра графа и определителя матрицы смежности.
