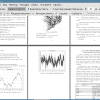
Тема: Программная реализация построения фрактального ряда и определения его показателя Херста
Закажите новую по вашим требованиям
Представленный материал является образцом учебного исследования, примером структуры и содержания учебного исследования по заявленной теме. Размещён исключительно в информационных и ознакомительных целях.
Workspay.ru оказывает информационные услуги по сбору, обработке и структурированию материалов в соответствии с требованиями заказчика.
Размещение материала не означает публикацию произведения впервые и не предполагает передачу исключительных авторских прав третьим лицам.
Материал не предназначен для дословной сдачи в образовательные организации и требует самостоятельной переработки с соблюдением законодательства Российской Федерации об авторском праве и принципов академической добросовестности.
Авторские права на исходные материалы принадлежат их законным правообладателям. В случае возникновения вопросов, связанных с размещённым материалом, просим направить обращение через форму обратной связи.
📋 Содержание
ВВЕДЕНИЕ 5
Глава 1 ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ФРАКТАЛЬНЫХ МНОЖЕСТВ 7
1.1 Основные понятия теории фракталов 7
1.2 Свойства фрактальных множеств 8
1.3 Фрактальная размерность 9
1.4 Показатель Херста 10
1.5 Самоподобие 11
1.6 Нахождение фрактальной размерности 12
Глава 2 МОДЕЛИРОВАНИЕ ФРАКТАЛЬНЫХ ВРЕМЕННЫХ РЯДОВ 14
2.1 Алгоритмы генерации фрактальных временных рядов 14
2.2 Реализация алгоритма смещения средней точки 18
Глава 3 АНАЛИЗ ФРАКТАЛЬНОЙ РАЗМЕРНОСТИ 21
3.1 Выделение периодичностей временных рядов 21
3.2 Алгоритмы методов анализа фрактальной размерности 22
3.3 Реализация алгоритма R/S -анализа 30
ЗАКЛЮЧЕНИЕ 37
СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ 38
ПРИЛОЖЕНИЕ A 41
ПРИЛОЖЕНИЕ Б 42
📖 Введение
Для их исследования используется теория фракталов и хаоса. Термин «фрактал» является статичной геометрической конфигурацией, как, например, снимок водопада. Хаос - это термин динамики, который используется для описания различных явлений, как, например, турбулентное поведение погоды.
Фракталы находят сейчас все больше и больше различных применений в науке и жизни человека, так как по сути все наше мироздание один большой фрактал. Фрактальная размерность, как индикатор нерегулярности графика фрактала, за последнее десятилетие вышла из области теоретической математики и стала важным количественным показателем в области обработки сигналов и изображений. Мера изрезанности контура объекта или нестационарности сигнала часто используется для получения важных характеристик данных, их классификации и прогнозирования. Фракталы используются для прогнозирования экономических индексов, разведочного анализа сигнала, медицинской диагностики, распознавания границ объектов и т.д. Этим и определяется актуальность темы исследования.
Объект исследования: фрактальные временные ряды.
Предмет исследования: компьютерное моделирование фрактальных временных рядов.
Цель данной работы - разработать программную реализацию построения фрактального ряда и программную реализацию определения показателя Херста.
Для реализации цели сформулированы следующие задачи:
1. Выявить и описать основные понятия, связанные с моделированием фрактальных рядов;
2. Осуществить анализ методов генерации фрактальных рядов и программную реализацию метода смещения средней точки;
3. Осуществить анализ методов определения размерности фракталов и программную реализацию определения показателя Херста.
В первой главе описываются основные понятия, связанные с моделированием и анализом временных рядов, вводятся понятия фрактальной размерности и показателя Херста.
Вторая глава посвящена способам построения фрактальных рядов. В первой части описываются алгоритмы построения фрактальных множеств. Во второй части выполняется реализация алгоритма смещения средней точки.
В третьей главе рассказывается о способах анализа фрактальных рядов, описываются некоторые методы нахождения показателя Херста, реализуется алгоритм R/S анализа.
✅ Заключение
В результате проделанной работы были разработаны программная реализация построения фрактального ряда методом смещения средней точки и программная реализация определения показателя Херста методом R/S-анализа.
При этом были решены следующие задачи.
Были выявлены и описаны основные понятия, связанные с моделированием фрактальных рядов.
Были рассмотрены некоторые популярные методы моделирования фракталов, такие как алгоритм смещения средней точки, обобщенное броуновское движение, L-системы, а так же выполнена компьютерная реализация алгоритма смещения средней точки.
Были рассмотрены такие методы анализа фрактальной размерности, как метод Ричардсона, метод Минковского, метод R/S -анализа, метод разложения в ряд Фурье, а так же выполнена компьютерная реализация метода R/S-анализа.